ディープラーニングにおけるロジット、Sigmoid、Softmax、クロスエントロピー損失の理解

機械学習でよく使われる関数の比較解説この記事は翻訳版です。訳の不備や誤訳がありましたら、コメント欄でお知らせください。
Created on August 26|Last edited on August 26
Comment
﻿
はじめにディープラーニングのモデルが、猫の画像と犬の画像をどうやって見分けているのか、不思議に思ったことはありますか？あるいは、ChatGPT を使っていて、次にどの単語を予測するのはどうやってわかるのだろう、と考えたことは？または、消費者からの苦情が届いたときに、ディープラーニングのモデルが自動的に適切な部署へ分類できた、という経験はないでしょうか。
すべての根底にあるのは、Softmax 関数、Sigmoid 関数、そしてクロスエントロピー損失の三本柱です。
データが「新しい石油」と言われ、AI があらゆる場面に浸透するいま、基礎を理解することはとても重要です。本記事では、その第一歩として一緒に学んでいきましょう。ロジット、Softmax と Sigmoid の活性化関数まず、ディープラーニングのネットワークでそれらがどのように広く使われているか、用途と利点は何かを理解し、そのうえで続きを見ていきましょう。クロスエントロピー損失。
本記事は理論偏重ではありません。数式には触れますが、PyTorch のコードを用いて用語を平易に説明します。内容をしっかり理解するには、Python の基礎知識があると大いに役立ちます。コードでは TIMM を使って画像分類モデルを作成し、ロジット、Softmax の活性化関数、クロスエントロピー損失、そして Sigmoid の活性化関数をより深く理解していきます。
💡
ロジットディープラーニングの文脈で「ロジット」という用語をよく耳にすると思います。しかし、ロジットとは何か？この定義は次のセクションでさらに明確になりますが、平たく言えば、ディープラーニングのネットワークの最終層から得られる生の出力はロジットと呼ばれます。ロジットまたは、より一般的には活性化値。
ディープラーニングのネットワークは基本的に行列積と非線形変換から成るため、これらの生の出力は次のように幅広い範囲を取り得ます。(−R,R)(-R, R)(−R,R)﻿どこでRは実数全体を表します。したがって、これらの生の出力は無限に負にも正にもなり得ます。
これらの生の出力はそのままではモデルのスコアとして解釈できないため、最終的なスコアを得る前に、これらの出力に対して活性化関数を適用します。
次の2つのセクションでは、そのような活性化関数を2つ取り上げ、詳しく見ていきます。シグモイドとソフトマックス—いくつかのサンプル問題を交えながら。
シグモイド関数たとえば、あなたが次の機械学習課題に取り組むデータサイエンティストだとします。
「入力画像が与えられたとき、その画像が車かどうかを判定せよ。」
では、このディープラーニングモデルの出力として一般的に何を望むでしょうか。望むのは、0 と 1 の間の数、ですよね。モデルがその入力画像を車だと判断するなら値は 1 に近いほどよく、車ではないと判断するなら値は 0 にできるだけ近いほうが望ましいはずです。
﻿
では、先ほど述べたように、ロジットは生の出力ディープラーニングのネットワークから得られるものであり、ディープラーニングのネットワークはすべて行列積と ReLU のような非線形性で構成されるため、ロジットの取りうる範囲は次のとおりです:[−R,R][-R, R][−R,R]﻿どこでRRR﻿実数全体を指す。
ただし、私たちが欲しい出力は 0 から 1 の間であり、無限に負にも正にもなりうる実数ではありません。では、ロジットをどのようにして 0 から 1 の値に変換すればよいのでしょうか。
答えはシグモイドです。これはディープラーニングの最終層の出力（ロジット）の後に一般的に用いられる活性化関数で、生の出力を 0 から 1 の範囲の値に変換します。
数学的には、シグモイド関数は次のように定義されます。
σ(t)=11+e−t\sigma(t) = \frac{1}{1 + e^{-t}}σ(t)=1+e−t1​﻿
この関数をプロットすると、次のような形になります。
﻿
上の図からわかるように、シグモイド関数の入力が 0 のときの出力は 0.5 です。σ(0)=0.5\sigma(0)=0.5σ(0)=0.5﻿、また、入力が -4 未満のときは出力は 0 に非常に近く、入力が 4 を超えると 1 に非常に近くなります。ロジットとシグモイド関数をコードで見てみましょう。TIMM を使ってディープラーニングモデルを作成します。
import timm, torch
﻿
x = torch.randn(1, 3, 224, 224)
m = timm.create_model('resnet18', num_classes=1)
m(x)
>> tensor([[-0.1522]], grad_fn=<AddmmBackward0>) #Logit
﻿
torch.sigmoid(m(x))
>> tensor([[0.4620]], grad_fn=<SigmoidBackward0>)
上の簡単なコード例からわかるように、モデルの最終層からの生の出力（ロジット）は -0.1522 ですが、これは確率としては解釈できません。そこでシグモイド関数を適用すると、最終的なスコアは 0.4620 になります。
以上がシグモイド関数の要点です。ここまでで、読者としてはロジットとシグモイド活性化関数が何かを理解できたはずです。要するに、ロジットはディープラーニングモデルの最終層から出る生の出力であり、シグモイドはそれらを 0 と 1 の間の最終的なスコアに変換する活性化関数です。
それでは、ソフトマックス活性化関数に進みましょう。
ソフトマックス活性化関数では、問題設定を更新しましょう。
「ある入力画像が与えられたとき、それが馬、ボール、魚、車、または棒のどれに当たるかを予測してください。」
ここでは、予測したい出力が単一クラスではなく複数クラスになります。各クラスの出力は 0 から 1 の範囲に収まり、さらにそれらの合計が 1 になることが望まれます。このような場合、シグモイド活性化関数ではこれらの性質を満たせません。
ここで読者の皆さんは、なぜシグモイド活性化関数では望む性質が得られないのか見当がつきますか。理由は、各スコアの合計が 1 になることを保証しないからです。シグモイド関数は、生のスコア（ロジット）を 0 から 1 の範囲に写像するだけで、その合計が 1 になることは保証しません。
💡
﻿
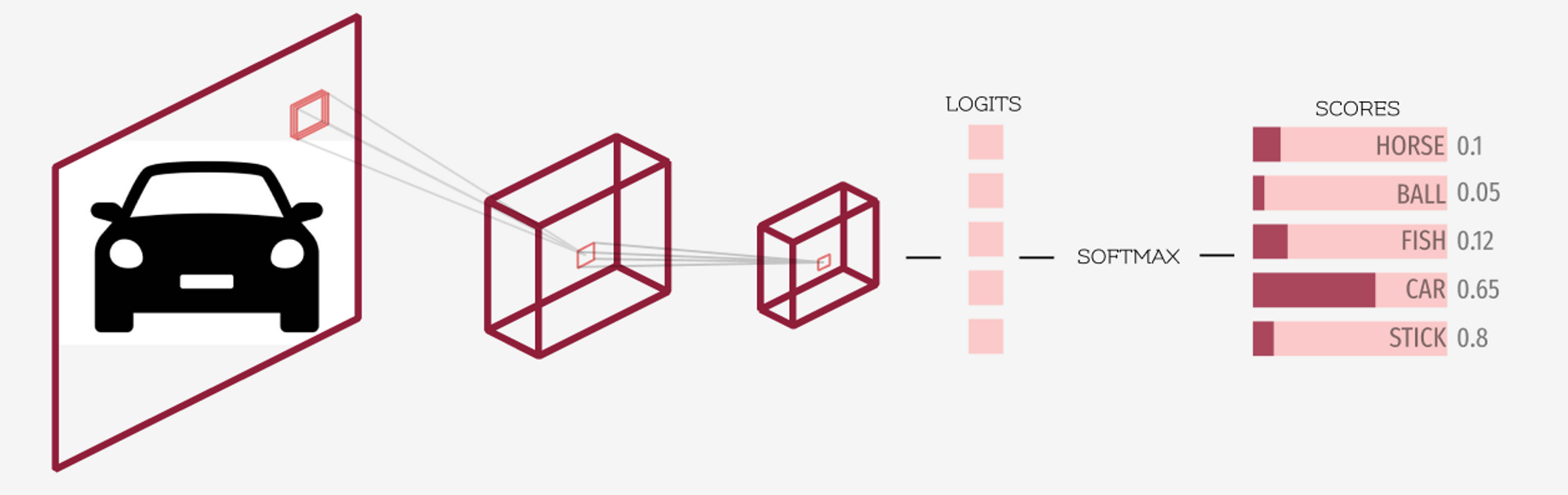
ロジットとソフトマックス活性化関数を明確に理解するために、上の画像を見てみましょう。前述のとおり、ディープラーニングモデルの最終層から得られる出力はロジットと呼ばれます。ソフトマックスは、これらのロジット（最終層の出力）に適用される活性化関数で、最終的なスコア／確率を得るために用いられます。これにより、各スコアは 0 から 1 の範囲に収まり、かつ合計が 1 になります。
コードでどのようになるか見てみましょう TIMM 最初に
import timm
import torch
﻿
m = timm.create_model('resnet18', num_classes=5)
x = torch.randn(1, 3, 224, 224)
logits = m(x)
logits 
 
>> tensor([[-0.2135, -0.0248,  3.985, -4.235, -0.1831]], grad_fn=<AddmmBackward0>)
﻿
scores = torch.softmax(logits)
scores 
﻿
>> tensor([[0.0096, 0.0117, 0.9765, 0.0002, 0.0020]], grad_fn=<SoftmaxBackward0>)
ご覧のとおり、ロジットはディープラーニングモデルの最終層から得られる生の出力です。ｍある入力画像が与えられたときx。
先に述べたとおり、ロジットは負の無限大から正の無限大までの実数全体の範囲を取り得ます。
💡
これらのロジットは正規化関数（たとえば Softmax）に渡され、その出力は必ず (0, 1) の範囲に収まり、全体の和が 1 になります。
Softmax の出力を段階的に計算する方法それでは、Softmax 関数について詳しく見ていきましょう。
softmax(Zi)=exp⁡(Zi)∑nexp⁡(Zj)\text{softmax}(Z_{i}) = \frac{\exp(Z_i)}{\sum_n \exp(Z_j)}softmax(Zi​)=∑n​exp(Zj​)exp(Zi​)​﻿
ある入力ベクトルが与えられたときZZZ﻿、softmax の値ZiZ_iZi​﻿に等しいeZi/(eZ1+eZ2+...+eZn)e^{Z_i}/(e^{Z_1} + e^{Z_2} + ... + e^{Z_n})eZi​/(eZ1​+eZ2​+...+eZn​)﻿全体が … であると仮定するとNNN﻿入力ベクトルの要素Z.Z.Z.﻿ 
では、TIMM を使って作成したニューラルネットワークの生の出力（ロジット）に、Softmax を適用してみましょう。
生の出力ロジットがベクトルに格納されていると仮定しますXこのベクトルの最初の要素の softmax の値を計算したいと思います。
﻿X=[−0.2135,−0.0248,3.985,−4.235,−0.1831]X = [-0.2135, -0.0248,  3.985, -4.235, -0.1831]X=[−0.2135,−0.0248,3.985,−4.235,−0.1831]﻿﻿
数式に従うと、
﻿softmax(−0.2135)=e−0.2135e−0.2135+e−0.0248+e3.985+e−4.235+e−0.1831\text{softmax}(-0.2135) = \frac{e^{-0.2135}}{e^{-0.2135} + e^{-0.0248} + e^{ 3.985} + e^{-4.235} + e^{-0.1831}}softmax(−0.2135)=e−0.2135+e−0.0248+e3.985+e−4.235+e−0.1831e−0.2135​﻿﻿
各項の指数を個別に先に計算すると、
﻿e−0.2135e^{-0.2135}e−0.2135﻿約0.8073
﻿e−0.0248e^{-0.0248}e−0.0248﻿約0.9754
﻿e0.3985e^{0.3985}e0.3985﻿約53.7032
﻿e−0.4235e^{
−0.4235}e−0.4235﻿約0.0144
﻿e−0.1831e^{−0.1831}e−0.1831﻿約0.8327
そして最終的な指数の合計は 56.3330 になります
したがって、Softmax(−0.2135)=0.8073/56.3330=0.0096\text{Softmax}(-0.2135) = 0.8073/56.3330 = 0.0096Softmax(−0.2135)=0.8073/56.3330=0.0096﻿﻿
したがって、最初の要素に対するSoftmax活性化関数の出力は-0.2135は0.0096 
Softmax関数の主な性質 
「どれか一つに絞り込む」性質があるため、ほとんどすべての分類タスクで最終的な正規化層として用いられます。
出力は常に〜の範囲になります0と1。
ソフトマックス関数の出力確率の合計は常に等しくなります1。
これは微分可能であり、バックプロパゲーションのような勾配に基づく最適化手法で使用できます。
これは、ロジット（実数値ベクトル）を確率分布に変換する方法として捉えることができます。
Softmax活性化関数は、単一のクラスを選び取る傾向がありますまず最初のポイントを見ていきましょう。これはソフトマックス関数を直感的に理解するうえで最も重要な点の一つです。Jeremy Howard が広く紹介しているように、 fast.ai コース 
﻿
﻿
ソフトマックス関数は、どれか一つに絞り込みたがります。なぜかというと、指数関数は値が大きくなるほど急激に増加するからです。
例えば、e4=54.5981e^4 = 54.5981e4=54.5981﻿一方でe8=2980.9579e^8=2980.9579e8=2980.9579﻿。では、ロジットがあるなら、あるロジットが他よりわずかに大きいだけでも、そのソフトマックスは他よりもずっと大きくなります。 
ロジットが与えられているとしましょう [0.02, -2.49, 1.25]これらの値の指数は [1.02, 0.08, 3.49]ソフトマックスの値は [0.22, 0.02,. 0.76]。ロジットのソフトマックスがどのようになるかがわかります 1.25 他のすべてよりもはるかに大きいです。 
これは望ましい性質ですよね。たとえば「この画像に写っているペットの品種はどれ？」とモデルに尋ねるとき、狙いは1つの品種に絞り込むことです。ソフトマックスはまさにそれを実現します。
負の対数尤度これまでにSigmoidとSoftmaxという活性化関数を見てきましたが、ここからは損失関数に目を向けましょう。具体的には、PyTorchの… torch.nll_loss 負の対数尤度損失という関数 
ここからは、モデルが実際に何を最適化しようとしているのかに目を向けます。私たちは損失を最小化するようにモデルを学習させますが、では多クラス分類ではそれがどのように機能するのでしょうか。
次の課題に取り組んでいるとしましょう。
「グリズリーベア、テディベア、ブラウンベアのいずれかが写った5枚の画像が与えられ、各画像を正しいクラスに分類するのがあなたの課題です。
これをPyTorchのコードで確認してみましょう。
import torch, timm 
import torch.nn.functional as F
﻿
classes = ['Grizzly', 'Brown', 'Teddy']
targets = [1, 0, 2, 0, 2] # these are your labels
[classes[idx] for idx in targets]
>> ['Brown', 'Grizzly', 'Teddy', 'Grizzly', 'Teddy']
つまり、ラベルによれば、最初の画像は…のものです。ブラウンベア次の画像は…のものです。グリズリーなど。
m = timm.create_model('resnet18', num_classes=3, pretrained=True)
x = torch.randn(5, 3, 224, 224) # five images of three channels of shape 224x224
logits = m(x)
logits
﻿
>>
tensor([[ 0.1752,  0.0539, -0.0581],
        [ 0.0544,  0.0642,  0.0782],
        [ 0.3230,  0.0958,  0.1941],
        [ 0.1143, -0.0508,  0.0701],
        [ 0.1249,  0.0510,  0.1147]], grad_fn=<AddmmBackward0>)
ご覧のとおり、ロジットはディープラーニングモデルの最終層から出力される生の値であり、範囲は[−R,R][-R, R][−R,R]﻿。
outputs = torch.softmax(logits, dim=1)
outputs 
﻿
>> 
tensor([[0.3734, **0.3308**, 0.2957],
        [**0.3296**, 0.3329, 0.3375],
        [0.3737, 0.2978, **0.3285**],
        [**0.3566**, 0.3023, 0.3411],
        [0.3426, 0.3182, **0.3391**]], grad_fn=<SoftmaxBackward0>)
﻿
idxs = torch.arange(5)
-outputs[idxs, targets]
>> tensor([-0.3308, -0.3296, -0.3285, -0.3566, -0.3391], grad_fn=<NegBackward0>)
さて、損失関数については、目標ラベルに基づいて上で強調した値に着目します。 [1, 0, 2, 0, 2]これらの値に負号を付けたものを負の対数尤度と呼びます。理想的には、これらの値ができるだけ大きく、1に近いことが望ましいです。 
これらの値に負号を付けたものは、PyTorch では次のように呼ばれます。 F.nll_loss。 
F.nll_loss(outputs, targets, reduction='none')
﻿
>> tensor([-0.3308, -0.3296, -0.3285, -0.3566, -0.3391], grad_fn=<NllLossBackward0>)
上で見たように、その出力は F.nll_loss 先ほど強調した値に負号を付けたものです。 
なお、上では対数を取っていません。 -outputs[idxs, targets] は、上で示した F.nll_loss と同じです。これは、PyTorch では softmax の出力に対して対数を取ってから F.nll_loss を適用する方が、はるかに高速だからです。 
💡
クロスエントロピー損失ロジットにソフトマックスを適用した後の対数は、次に続く F.nll_loss クロスエントロピー損失と呼ばれます。
難しそうに聞こえますか？段階に分ければ難しくありません。以下の4ステップが、クロスエントロピー損失の完全な定義です。
ロジット（モデルの最終層から出力される生の値）を計算する
ロジットにソフトマックスを適用する。 
ステップ2の出力に対数を取る。 
計算する F.nll_loss 先ほどと同様に、ステップ3の出力とターゲット値を渡してインデックスを取るだけです。
では、コードで確認してみましょう。
import torch, timm 
import torch.nn.functional as F
﻿
############################## step=1 ##############################
classes = ['Grizzly', 'Brown', 'Teddy']
targets = [1, 0, 2, 0, 2] # these are your labels
m = timm.create_model('resnet18', num_classes=3, pretrained=True)
x = torch.randn(5, 3, 224, 224) # five images of three channels of shape 224x224
logits = m(x)
logits
>>
tensor([[ 0.1752,  0.0539, -0.0581],
        [ 0.0544,  0.0642,  0.0782],
        [ 0.3230,  0.0958,  0.1941],
        [ 0.1143, -0.0508,  0.0701],
        [ 0.1249,  0.0510,  0.1147]], grad_fn=<AddmmBackward0>)
ここまでで、モデルから生の出力（ロジット）が得られました。
############################## step=2 ##############################
﻿
torch.softmax(logits, dim=1)
>> 
tensor([[0.3734, 0.3308, 0.2957],
        [0.3296, 0.3329, 0.3375],
        [0.3737, 0.2978, 0.3285],
        [0.3566, 0.3023, 0.3411],
        [0.3426, 0.3182, 0.3391]], grad_fn=<SoftmaxBackward0>)
では、次のステップとして対数を取ります。
############################## step=3 ##############################
torch.log(torch.softmax(logits, dim=1))
>> 
tensor([[-0.9850, -1.1062, -1.2183],
        [-1.1099, -1.1001, -1.0861],
        [-0.9842, -1.2115, -1.1132],
        [-1.0312, -1.1963, -1.0755],
        [-1.0711, -1.1450, -1.0813]], grad_fn=<LogBackward0>)
最後に、ターゲットとステップ3の出力を渡して、PyTorchで負の対数尤度を計算します。
############################## step=4 ##############################
F.nll_loss(torch.log(torch.softmax(logits, dim=1)), torch.tensor(targets), reduction='none')
﻿
>> tensor([1.1062, 1.1099, 1.1132, 1.0312, 1.0813], grad_fn=<NllLossBackward0>)
これはクロスエントロピー損失と同じですでは、PyTorchを使ってクロスエントロピー損失の出力と比較してみましょう。
import torch.nn as nn
loss_fn = nn.CrossEntropyLoss(reduction='none')
loss_fn(logits, targets)
﻿
>> tensor([1.1062, 1.1099, 1.1132, 1.0312, 1.0813], grad_fn=<NllLossBackward0>)
ご覧のとおり、出力は同じです。したがって、クロスエントロピー損失を段階的に正しく計算できました。先ほど述べたように、「ロジットにソフトマックスを適用した後の対数は、次に続く F.nll_loss クロスエントロピー損失と呼ばれます。」
なお、PyTorch には次の関数が用意されています torch.log_softmax として使用できます torch.log(torch.softmax(...))。
💡
まとめ本記事では、ディープラーニングにおけるロジットの意味を説明しました。平たく言えば、ロジットとはニューラルネットワークの最終層から出力される生の値（未加工の出力）のことです。
次に、Sigmoid と Softmax の活性化関数についても見てきました。Sigmoid 活性化関数は、生の値をすべて次の範囲のスコアに変換できます: (−1,1)(-1, 1)(−1,1)﻿Softmax でも同様の変換は可能ですが、出力の総和が 1 になることも保証します。したがって、2値分類やマルチラベル分類には sigmoid が、モデルに単一のクラスを選ばせたい多クラス分類には softmax が一般に適しています。
最後に、PyTorch の負の対数尤度関数を確認し、4つの簡単な手順でクロスエントロピー損失を計算しました。これにより、読者の皆さんがこれらの概念を明瞭かつすっきり理解できたことを願っています。
﻿
﻿
Add a comment