Understanding Logits, Sigmoid, Softmax, and Cross-Entropy Loss in Deep Learning

機械学習でよく使われる関数を比較する解説記事です。この記事は翻訳版です。誤訳に気付かれた場合はコメント欄で報告してください。
Created on August 26|Last edited on August 26
Comment
﻿
導入深層学習モデルがどうやって猫の画像と犬の画像を区別できるのか、不思議に思ったことはありませんか？あるいは ChatGPT を使っていて、次にどの単語を予測するかをどうやって判断しているのか疑問に思ったことはありませんか？または、消費者からの苦情が届いたときに、深層学習モデルが自動的に正しい部署に分類できた、という経験はないでしょうか。
すべての根底にあるのは、ソフトマックス関数、シグモイド関数、そして交差エントロピー損失という三つ組です！
データが石油のように価値を持ち、AIが至る所に存在する現代では、基礎を理解することが重要です。本記事では、一緒に次のことを学ぶ旅に出ましょう。ロジット、ソフトマックスとシグモイドの活性化関数まず、深層学習のネットワーク全体でどのように使われているか、どんな用途や利点があるかを理解し、その後で…交差エントロピー損失。
この記事は理論中心ではありません。いくつかの数式に触れますが、PyTorch のコードを使って分かりやすく説明します。Python の基本的な知識があれば、本記事やそこで扱う概念をよりよく理解できます。コード例では TIMM を使って画像分類モデルを作成し、ロジット、ソフトマックス活性化関数、交差エントロピー損失、シグモイド活性化関数を詳しく確認していきます。
💡
ロジット深層学習の文脈で「ロジット」という用語はよく耳にするはずです。しかし、ロジットとは何ですか？この定義は次の章でさらに明確になりますが、簡単に言うと：深層学習ネットワークの最終層からの生の出力は「ロジット」と呼ばれますロジットまたは、より一般的には〜とも呼ばれます活性化出力。
深層学習ネットワークは基本的に行列積と非線形変換から成るため、これらの生の出力は非常に大きな値や非常に小さな値など、幅広い値を取り得ます。(−R,R)(-R, R)(−R,R)﻿どこでRは実数を表します。したがって、これらの生の出力は負にも正にも無限に広がる値を取り得ます。
これらの生の出力はそのままモデルのスコアとして解釈できないため、最終的なスコアを得る前にこれらの出力に活性化関数を適用します。
次の二節では、そうした活性化関数のうち二つを詳しく見ていきます。シグモイドそしてソフトマックス—サンプル問題の助けを借りて。
シグモイド関数あなたがこの機械学習の問題に取り組んでいるデータサイエンティストだとしましょう：
入力画像が与えられたとき、その画像が車であるかどうかを予測する。
さて、このディープラーニングモデルの出力として一般的に何を求めるでしょうか。あなたが欲しいのは、0から1の間の数値ですよね？モデルが入力画像を車だと判断するほどその数値は1に近く、車でないと判断するほど0に近い値になってほしいはずです。
﻿
先ほど述べたように、ロジットは生の出力値であり、制約のない実数です。生の出力ディープラーニングネットワークの出力であり、すべてのディープラーニングネットワークは行列の掛け算と ReLU のような非線形性から成るため、ロジットの値の範囲は実数全体に及びます[−R,R][-R, R][−R,R]﻿どこでRRR﻿実数を指します。
しかし、出力は実数で無限に大きくなったり小さくなったりするのではなく、0から1の範囲に収めたいことを忘れてはいけません。では、ロジットをどうやって0〜1の数値に変換するのでしょうか。
答えはシグモイドです。これはディープラーニングの最終層の出力（ロジット）の後によく使われる活性化関数で、生の出力を0〜1の値に変換��ます。
数学的には、シグモイド関数は次のように定義されます：
σ(t)=11+e−t\sigma(t) = \frac{1}{1 + e^{-t}}σ(t)=1+e−t1​﻿
関数をプロットすると、次のようになります。
﻿
上の図からわかるように、シグモイド関数の入力が0のときの出力値は0.5ですσ(0)=0.5\sigma(0)=0.5σ(0)=0.5﻿入力が-4未満では値はほぼ0に、4より大きいとほぼ1になります。ではロジットとシグモイド関数をコードで見てみましょう。深層学習モデルの作成にはTIMMを使います：
import timm, torch
﻿
x = torch.randn(1, 3, 224, 224)
m = timm.create_model('resnet18', num_classes=1)
m(x)
>> tensor([[-0.1522]], grad_fn=<AddmmBackward0>) #Logit
﻿
torch.sigmoid(m(x))
>> tensor([[0.4620]], grad_fn=<SigmoidBackward0>)
上の簡単なコード例からわかるように、モデルの最終層の生の出力は -0.1522 ですが、これは確率としてそのまま解釈できません。そこでシグモイド関数を適用すると、最終的なスコアは 0.4620 になります。
以上がシグモイド関数の全てです。ここまでで、読者のあなたはロジットとシグモイド活性化の意味を理解できています。要するに、ロジットはディープラーニングモデルの最終層から出る生の出力であり、シグモイドはそれらの生出力を0〜1の範囲の最終スコアに変換する活性化関数です。
次はソフトマックス活性化関数に進みましょう。
ソフトマックス活性化関数それでは問題文を更新しましょう：
「ある入力画像に対して、その画像が馬、ボール、魚、車、または棒のどれであるかを予測します。”
ここでは予測対象のクラスが1つだけではなく複数あります。各クラスに対する出力は0〜1の範囲で、かつそれらの合計が1になるようにしたいです。そのため、シグモイド関数ではこれらの条件を満たせません。
読者のあなたは、なぜシグモイド活性化関数では望む結果が得られないか推測できますか？答えは、スコアの合計が1になることを保証しないからです。シグモイド関数は生のスコアを0〜1の範囲に変換するだけで、合計が1になるようには調整しません。
💡
﻿
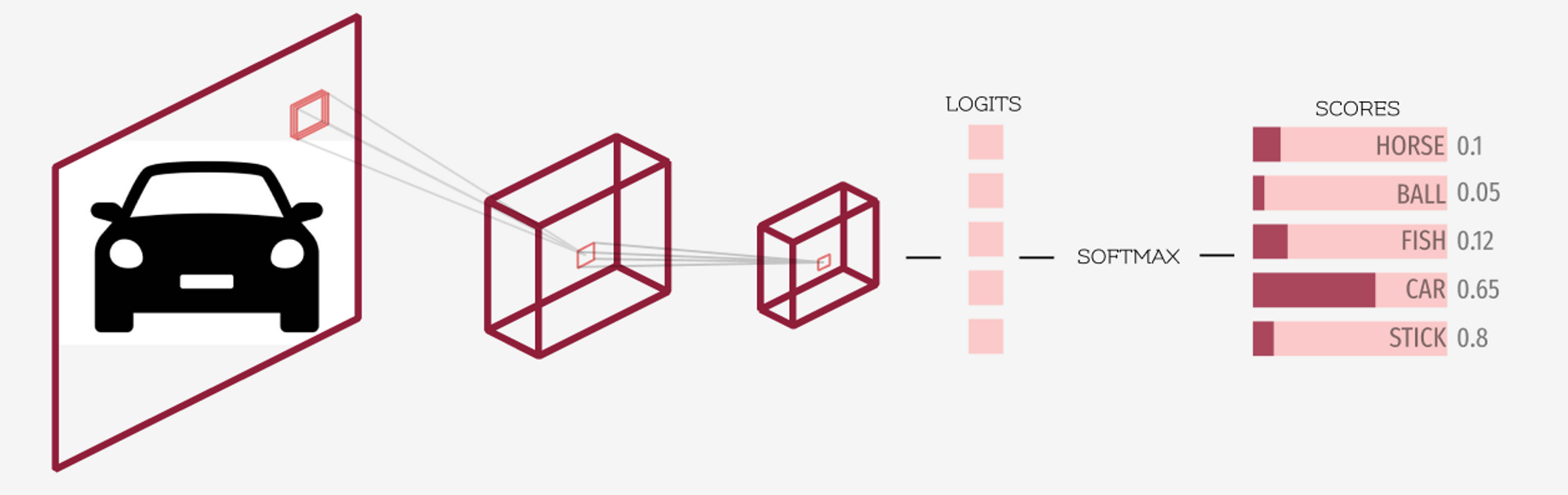
上の図を見て、ロジットとソフトマックス活性化関数をはっきり理解しましょう。先に述べたように、深層学習モデルの最終層から得られる出力はロジットと呼ばれます。ソフトマックスはロジット（最終層の出力）に適用される活性化関数で、各クラスの最終的なスコア／確率を得るために用いられます。これにより各スコアは0〜1の範囲になり、全てのスコアの合計は1になります。
これをコードで見てみましょう。 TIMM 最初：
import timm
import torch
﻿
m = timm.create_model('resnet18', num_classes=5)
x = torch.randn(1, 3, 224, 224)
logits = m(x)
logits 
 
>> tensor([[-0.2135, -0.0248,  3.985, -4.235, -0.1831]], grad_fn=<AddmmBackward0>)
﻿
scores = torch.softmax(logits)
scores 
﻿
>> tensor([[0.0096, 0.0117, 0.9765, 0.0002, 0.0020]], grad_fn=<SoftmaxBackward0>)
上で見たように、ロジットは深層学習モデルからの生の出力ですｍある入力画像が与えられたときx。
前述のとおり、ロジットは負の無限大から正の無限大までの任意の実数値を取り得ます。
💡
これらのロジットはその後ソフトマックスのような正規化関数に渡されます。ソフトマックスの出力はそれぞれが0〜1の範囲に収まり、全ての出力の合計は1になります。
ソフトマックス出力の段階的計算次に、ソフトマックス関数を詳しく理解し見ていきましょう。
softmax(Zi)=exp⁡(Zi)∑nexp⁡(Zj)\text{softmax}(Z_{i}) = \frac{\exp(Z_i)}{\sum_n \exp(Z_j)}softmax(Zi​)=∑n​exp(Zj​)exp(Zi​)​﻿
ある入力ベクトルが与えられたときZZZ﻿、ソフトマックスの値ZiZ_iZi​﻿に等しいeZi/(eZ1+eZ2+...+eZn)e^{Z_i}/(e^{Z_1} + e^{Z_2} + ... + e^{Z_n})eZi​/(eZ1​+eZ2​+...+eZn​)﻿合計があると仮定してNNN﻿入力ベクトル内の要素Z.Z.Z.﻿ 
では、TIMMで作成したニューラルネットワークから得られた生の出力（logits）に対して、まずソフトマックスを適用してみましょう。
生の出力であるロジットがベクトルに格納されていると仮定しましょうXこのベクトルの最初の要素に対するソフトマックス値を計算してみましょう。
﻿X=[−0.2135,−0.0248,3.985,−4.235,−0.1831]X = [-0.2135, -0.0248,  3.985, -4.235, -0.1831]X=[−0.2135,−0.0248,3.985,−4.235,−0.1831]﻿﻿
数学的な式に従うと：
﻿softmax(−0.2135)=e−0.2135e−0.2135+e−0.0248+e3.985+e−4.235+e−0.1831\text{softmax}(-0.2135) = \frac{e^{-0.2135}}{e^{-0.2135} + e^{-0.0248} + e^{ 3.985} + e^{-4.235} + e^{-0.1831}}softmax(−0.2135)=e−0.2135+e−0.0248+e3.985+e−4.235+e−0.1831e−0.2135​﻿﻿
各項の指数をまず個別に計算する：
﻿e−0.2135e^{-0.2135}e−0.2135﻿約0.8073
﻿e−0.0248e^{-0.0248}e−0.0248﻿約0.9754
﻿e0.3985e^{0.3985}e0.3985﻿約53.7032
﻿e−0.4235e^{
−0.4235}e−0.4235﻿約0.0144
﻿e−0.1831e^{−0.1831}e−0.1831﻿約0.8327
そして最後に指数の合計は約56.3330になります。
したがって、Softmax(−0.2135)=0.8073/56.3330=0.0096\text{Softmax}(-0.2135) = 0.8073/56.3330 = 0.0096Softmax(−0.2135)=0.8073/56.3330=0.0096﻿﻿
したがって、ソフトマックス活性化関数の出力は最初の要素に対して次のようになります。約-0.2135です約0.0096 
ソフトマックス関数の性質のいくつか： 
ほとんどすべての分類問題の最後に、最終的な正規化層として「あるクラスを選ぶ」ために使われます。
出力は常に...の間になります0そして1。
ソフトマックス関数の出力確率の総和は常に1になります。1。
これは微分可能であり、バックプロパゲーションのような勾配に基づく最適化手法で利用できます。
ロジット（実数値ベクトル）を確率分布に変換する方法と見なせます。
ソフトマックス活性化関数は単一のクラスを選びたがりますまず最初の点を見てみましょう。これはソフトマックス関数について直感的に理解するうえで最も重要なポイントの一つです。ジェレミー・ハワードがよく紹介しているように、 fast.ai コース： 
﻿
﻿
ソフトマックス関数は一つの候補を選びたがります。なぜなら、ある値の指数関数は非常に速く増大するからです。
例えば、e4=54.5981e^4 = 54.5981e4=54.5981﻿一方でe8=2980.9579e^8=2980.9579e8=2980.9579﻿つまり、ロジットがある場合、一つのロジットが他より少し大きいだけでも、そのソフトマックスは他の値よりずっと大きくなります。 
いくつかのロジットが与えられているとしましょう。 [0.02, -2.49, 1.25]これらの値の指数関数は... [1.02, 0.08, 3.49]ソフトマックスの値は [0.22, 0.02,. 0.76]ロジットのソフトマックスがどのようになるかが分かります。 1.25 他のすべてよりずっと大きい。 
それでいいんですよね？ 「この画像のペットはどの品種か？」とモデルに尋ねるような場合、モデルには一つの品種を選んでほしいはずです。だからこそソフトマックスが使われます。
負の対数尤度以前にシグモイドとソフトマックスの活性化関数を見たので、次は損失関数を見ていきます。具体的には、PyTorch の... torch.nll_loss 負の対数尤度損失関数 
始める前に、モデルが本当に何を最適化しようとしているのかを見ていきます。モデルは損失を最小化するように学習しますが、多クラス分類問題ではどう動くのでしょうか？
次の問題に取り組んでいるとしましょう：
「あなたにはグリズリーベア、テディベア、ブラウンベアのいずれかの画像が5枚与えられ、それらを正しいクラスに分類することが仕事です。
では、これをPyTorchのコードで見てみましょう：
import torch, timm 
import torch.nn.functional as F
﻿
classes = ['Grizzly', 'Brown', 'Teddy']
targets = [1, 0, 2, 0, 2] # these are your labels
[classes[idx] for idx in targets]
>> ['Brown', 'Grizzly', 'Teddy', 'Grizzly', 'Teddy']
これはラベルによれば、最初の画像がそのクラスに属することを意味します。ブラウンベア、2番目の画像はそのクラスに属することを意味します。グリズリーベア、など。
m = timm.create_model('resnet18', num_classes=3, pretrained=True)
x = torch.randn(5, 3, 224, 224) # five images of three channels of shape 224x224
logits = m(x)
logits
﻿
>>
tensor([[ 0.1752,  0.0539, -0.0581],
        [ 0.0544,  0.0642,  0.0782],
        [ 0.3230,  0.0958,  0.1941],
        [ 0.1143, -0.0508,  0.0701],
        [ 0.1249,  0.0510,  0.1147]], grad_fn=<AddmmBackward0>)
上の図が示すように、ロジットはディープラーニングモデルの生の出力であり、値は実数で非常に大きくなったり小さくなったりします。[−R,R][-R, R][−R,R]﻿。
outputs = torch.softmax(logits, dim=1)
outputs 
﻿
>> 
tensor([[0.3734, **0.3308**, 0.2957],
        [**0.3296**, 0.3329, 0.3375],
        [0.3737, 0.2978, **0.3285**],
        [**0.3566**, 0.3023, 0.3411],
        [0.3426, 0.3182, **0.3391**]], grad_fn=<SoftmaxBackward0>)
﻿
idxs = torch.arange(5)
-outputs[idxs, targets]
>> tensor([-0.3308, -0.3296, -0.3285, -0.3566, -0.3391], grad_fn=<NegBackward0>)
さて、損失関数については、目標ラベルに基づいて上で強調表示した値に注目します。 [1, 0, 2, 0, 2]これらの値の負をとったものは負の対数尤度と呼ばれます。理想的には、これらの値は大きく、1に近いことが望まれます。 
これらの値の負を取ると、PyTorchではこれがF.nll_lossとして呼ばれます。 F.nll_loss。 
F.nll_loss(outputs, targets, reduction='none')
﻿
>> tensor([-0.3308, -0.3296, -0.3285, -0.3566, -0.3391], grad_fn=<NllLossBackward0>)
上に示したように、出力は F.nll_loss これは前に強調表示した値の負の値です。 
上では対数を取っていないことに注意してください。 -outputs[idxs, targets] これは上で示したF.nll_lossと同じです。PyTorchでは、ソフトマックス出力の後で対数を取り、それからF.nll_lossを適用する方が高速であるためです。 
💡
クロスエントロピー損失ロジットに対するソフトマックスの対数の後に F.nll_loss これは Cross Entropy Loss と呼ばれます。
複雑に聞こえますか？ 手順に分ければそうでもありません。以下の四つのステップがクロスエントロピー損失の完全な定義です。
ロジット（モデルの最終層からの生の出力）を計算する
ロジットに対してソフトマックスを適用する。 
ステップ2の出力に対して対数を取る。 
計算する F.nll_loss これは前に示したように単純にインデックス指定を行うもので、ステップ3の出力と目的ラベルを渡して実行します。
では、実際にコードで見てみましょう。
import torch, timm 
import torch.nn.functional as F
﻿
############################## step=1 ##############################
classes = ['Grizzly', 'Brown', 'Teddy']
targets = [1, 0, 2, 0, 2] # these are your labels
m = timm.create_model('resnet18', num_classes=3, pretrained=True)
x = torch.randn(5, 3, 224, 224) # five images of three channels of shape 224x224
logits = m(x)
logits
>>
tensor([[ 0.1752,  0.0539, -0.0581],
        [ 0.0544,  0.0642,  0.0782],
        [ 0.3230,  0.0958,  0.1941],
        [ 0.1143, -0.0508,  0.0701],
        [ 0.1249,  0.0510,  0.1147]], grad_fn=<AddmmBackward0>)
では、モデルからの生の出力（ロジット）が得られました。
############################## step=2 ##############################
﻿
torch.softmax(logits, dim=1)
>> 
tensor([[0.3734, 0.3308, 0.2957],
        [0.3296, 0.3329, 0.3375],
        [0.3737, 0.2978, 0.3285],
        [0.3566, 0.3023, 0.3411],
        [0.3426, 0.3182, 0.3391]], grad_fn=<SoftmaxBackward0>)
では、次のステップとして対数を取る必要があります。
############################## step=3 ##############################
torch.log(torch.softmax(logits, dim=1))
>> 
tensor([[-0.9850, -1.1062, -1.2183],
        [-1.1099, -1.1001, -1.0861],
        [-0.9842, -1.2115, -1.1132],
        [-1.0312, -1.1963, -1.0755],
        [-1.0711, -1.1450, -1.0813]], grad_fn=<LogBackward0>)
最後に、PyTorch を使って負の対数尤度を計算します。ターゲットとステップ3の出力を渡してください。
############################## step=4 ##############################
F.nll_loss(torch.log(torch.softmax(logits, dim=1)), torch.tensor(targets), reduction='none')
﻿
>> tensor([1.1062, 1.1099, 1.1132, 1.0312, 1.0813], grad_fn=<NllLossBackward0>)
これは Cross Entropy Loss と同じですでは、PyTorch の Cross Entropy Loss の出力と結果を比較してみましょう。
import torch.nn as nn
loss_fn = nn.CrossEntropyLoss(reduction='none')
loss_fn(logits, targets)
﻿
>> tensor([1.1062, 1.1099, 1.1132, 1.0312, 1.0813], grad_fn=<NllLossBackward0>)
ご覧のとおり、出力は同じです。これで Cross Entropy Loss をステップごとに正しく計算できました。先に述べたように、ロジットに対するソフトマックスの対数の後に F.nll_loss これは Cross Entropy Loss と呼ばれます。”
PyTorch には、という関数が用意されていることに注意してください。 torch.log_softmax 置き換えとして使用できる torch.log(torch.softmax(...))。
💡
結論このブログ記事では、ディープラーニングの文脈でロジットが何を意味するかを説明しました。平易に言えば、ロジットとはディープラーニングモデルの最終層から出力される未加工の値のことです。
次に、Sigmoid と Softmax の活性化関数についても見ていきました。Sigmoid は生の値をすべて 0〜1 の範囲のスコアに変換できます。 (−1,1)(-1, 1)(−1,1)﻿Softmax も同様の変換を行いますが、出力が合計で 1 になることを保証します。したがって、シグモイドは二値分類やマルチラベル分類で好んで使われ、モデルに「ひとつのクラスを選ばせたい」多クラス分類ではソフトマックスが好まれます。
最後に、PyTorch の負の対数尤度関数を見て、4つの簡単なステップでクロスエントロピー損失を計算しました。これにより、読者の皆さんがこれらの概念を明確かつすっきりと理解できたことを願っています。🙂
﻿
﻿
Add a comment