Skip to main content
wandb_fc
Projects
korean
Reports
딥러닝 분류의 핵심 개념: 로짓, 시그모이드, 소프트맥스, 크로스 엔트로피 손실 이해하기

딥러닝 분류의 핵심 개념: 로짓, 시그모이드, 소프트맥스, 크로스 엔트로피 손실 이해하기

ML에서 흔히 사용되는 함수들을 비교해 설명합니다 이 글은 AI 번역 기사입니다. 오역이 의심되면 댓글로 알려주세요
Aman Arora
Created on September 12|Last edited on September 12

소개

딥러닝 모델이 어떻게 고양이 이미지와 개 이미지를 구분하는지 궁금해본 적이 있나요? 혹은 ChatGPT를 쓰면서 다음에 어떤 단어를 예측해야 하는지 어떻게 아는지 의문이 들었던 적이 있나요? 또는 소비자 불만이 접수되었을 때 딥러닝 모델이 자동으로 해당 부서로 정확히 분류하는 경우를 본 적이 있을지도 모릅니다.
이 모든 것의 핵심에는 Softmax 함수, Sigmoid 함수, 그리고 Cross-Entropy Loss라는 세 가지가 있습니다!
데이터가 석유라 불리고 AI가 곳곳에 스며든 오늘날, 기본기를 이해하는 것이 중요합니다. 이 블로그 글에서 우리는 함께 다음 내용을 배우는 여정을 떠나보겠습니다. 로짓, softmax와 sigmoid 활성화 함수 먼저, 이들이 딥러닝 네트워크 전반에서 어떻게 쓰이는지, 각 용례와 장점은 무엇인지 이해한 뒤, 이어서 다음 내용�� 살펴보겠습니다. cross-entropy loss.
이 블로그 글은 이론서가 아닙니다! 몇 가지 수식을 언급하더라도, PyTorch 코드를 활용해 독자가 이해하기 쉽도록 용어를 간단히 설명하겠습니다. 이 글과 그 안에서 다루는 개념을 온전히 이해하려면 Python에 대한 어느 정도의 숙련도가 큰 도움이 됩니다. 코드에서는 TIMM을 사용해 이미지 분류 모델을 만들며, 이를 통해 logits, softmax 활성화 함수, cross-entropy loss, sigmoid 활성화 함수를 더 깊이 이해해 보겠습니다.
💡

로짓

딥러닝 맥락에서 logit이라는 용어를 많이 들어보셨을 겁니다. 하지만, 로짓이란 무엇인가요? 이 정의는 다음 섹션에서 더 명확해지겠지만, 간단히 말해 딥러닝 네트워크의 마지막 층에서 나오는 원시 출력값을 가리켜 로짓이라고 합니다. 로짓 또는 더 흔히 불리는 활성화 함수.
딥러닝 네트워크는 가장 기본적으로 행렬 곱셈과 비선형 함수로 구성되므로, 이러한 원시 출력값은 다음과 같은 범위를 가질 수 있습니다 (−R,R)(-R, R) 어디에서 알 실수를 나타냅니다. 따라서 이러한 원시 출력값은 무한히 음수가 될 수도 있고 양수가 될 수도 있습니다.
이러한 원시 출력값은 모델의 점수로 바로 해석할 수 없기 때문에, 최종 점수를 얻기 전에 이 값들 위에 적용하는 활성화 함수가 필요합니다.
다음 두 개의 섹션에서는 이러한 활성화 함수 두 가지를 자세히 살펴보겠습니다—시그모이드 그리고 소프트맥스—샘플 문제를 통해 살펴보겠습니다.

시그모이드 함수

당신이 다음과 같은 머신러닝 문제를 다루는 데이터 사이언티스트라고 가정해 봅시다:
입력 이미지가 주어졌을 때, 그 이미지가 자동차인지 아닌지 예측하시오.
그렇다면 이 딥러닝 모델의 출력으로 보통 무엇을 원할까요? 여러분이 원하는 것은 0과 1 사이의 수그렇죠? 모델이 입력 이미지가 자동차라고 판단하면 그 수가 1에 가깝기를, 자동차가 아니라고 판단하면 그 수가 0에 최대한 가깝기를 원할 것입니다.

이제 앞서 언급했듯이, 로짓은 원시 출력 딥러닝 네트워크의 출력이며, 모든 딥러닝 네트워크는 행렬 곱셈과 ReLU 같은 비선형 함수를 포함하므로, 로짓의 범위는 다음과 같습니다. [−R,R][-R, R] 어디에서 RR 실수를 가리킵니다.
하지만 우리는 출력이 무한히 음수나 양수가 될 수 있는 실수가 아니라 0과 1 사이에 있기를 원한다는 점을 기억하세요. 그렇다면 로짓�� 0과 1 사이의 수로 어떻게 변환할 수 있을까요?
정답은 시그모이드입니다. 이는 딥러닝의 마지막 층 출력(로짓) 뒤에 흔히 사용하는 활성화 함수로, 원시 출력을 0과 1 사이의 값으로 변환합니다.
수학적으로 말하면, 시그모이드 함수는 다음과 같이 정의됩니다:
σ(t)=11+e−t\sigma(t) = \frac{1}{1 + e^{-t}}

함수를 그래프로 그리면 아래와 같습니다:

위에서 볼 수 있듯이, 시그모이드 함수의 0에서의 출력 값은 0.5입니다. σ(0)=0.5\sigma(0)=0.5, 그리고 입력이 -4 미만이면 값이 0에 매우 가깝고, 입력이 4 초과이면 1에 가깝습니다. 이제 코드에서 logit과 sigmoid 함수를 살펴보겠습니다. 딥러닝 모델을 만들기 위해 TIMM을 사용하겠습니다:
import timm, torch

x = torch.randn(1, 3, 224, 224)
m = timm.create_model('resnet18', num_classes=1)
m(x)
>> tensor([[-0.1522]], grad_fn=<AddmmBackward0>) #Logit

torch.sigmoid(m(x))
>> tensor([[0.4620]], grad_fn=<SigmoidBackward0>)
위의 간단한 코드 예시에서 볼 수 있듯이, 모델 마지막 층의 원시 출력값은 -0.1522이지만 이는 확률 점수로 직접 해석할 수 없습니다. 따라서 시그모이드 함수를 적용하면 최종 점수는 0.4620이 됩니다.
시그모이드 함수는 여기까지입니다. 지금까지 독자인 여러분은 로짓과 시그모이드 활성화 함수가 무엇인지 이해하셨습니다. 요약하면, 로짓은 딥러닝 모델 마지막 층에서 나온 원시 출력이고, 시그모이드는 이 원시 출력을 0과 1 사이의 최종 점수로 변환하는 활성화 함수입니다.
이제 소프트맥스 활성화 함수로 넘어가 봅시다.

소프트맥스 활성화 함수

이제 문제 정의를 업데이트해 봅시다:
”어떤 입력 이미지가 주어졌을 때, 그것이 말, 공, 물고기, 자동차, 또는 막대기인지 예측하세요.”
여기서는 예측하려는 출력이 단일 클래스 하나가 아니라 여러 클래스입니다. 각 클래스의 출력이 0과 1 사이에 있고, 이 점수들의 합이 1이 되도록 만들어야 합니다. 이런 경우에는 시그모이드 활성화 함수만으로는 이러한 특성을 만족시킬 수 없습니다.
독자 여러분은 왜 시그모이드 활성화 함수를 쓰면 우리가 원하는 성질을 얻지 못하는지 짐작할 수 있을까요? 그 이유는 점수들의 합이 1이 되도록 보장하지 않기 때문입니다. 시그모이드 함수는 각 원시 점수를 0과 1 사이로만 변환할 뿐, 그 합이 1이 되도록 하지는 않습니다.
💡

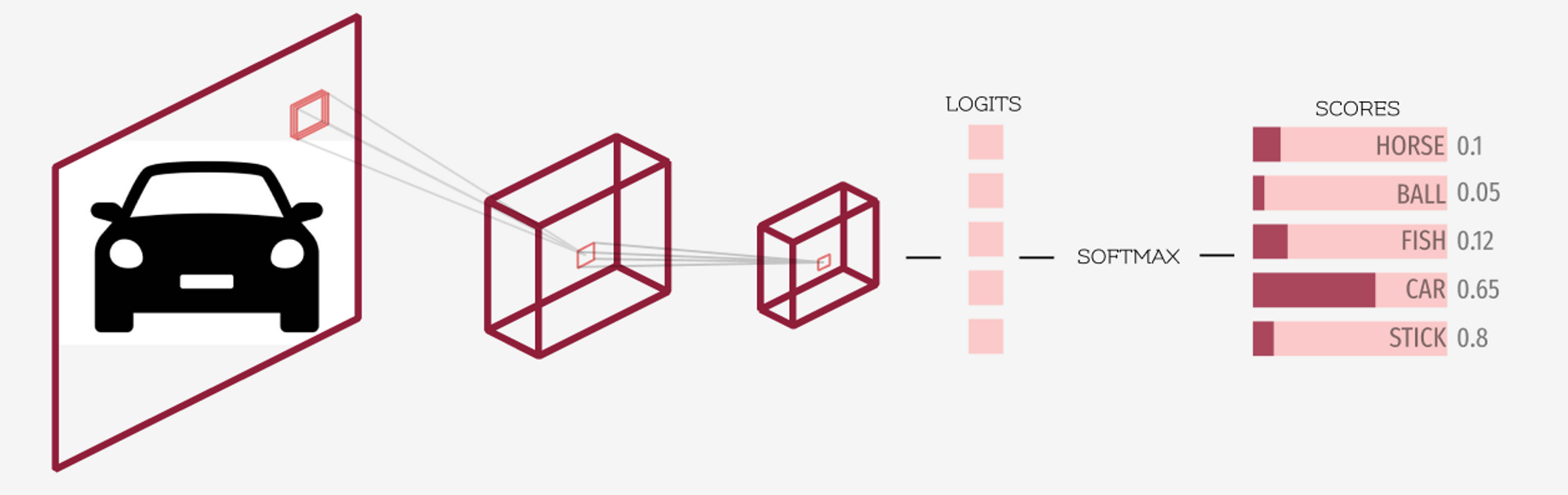
위의 이미지를 보면서 로짓과 소프트맥스 활성화 함수를 명확히 이해해 봅시다. 앞서 언급했듯이, 딥러닝 모델의 마지막 층에서 나오는 출력은 로짓이라고 부릅니다. 소프트맥스는 로짓(마지막 층의 출력)에 적용되는 활성화 함수로, 최종 점수/확률을 얻기 위해 사용되며, 이때 각 최종 점수는 0과 1 사이에 있고 전체 합은 1이 되도록 보장합니다.
이것을 코드로 어떻게 구현하는지 살펴봅시다 using TIMM 먼저:
import timm
import torch

m = timm.create_model('resnet18', num_classes=5)
x = torch.randn(1, 3, 224, 224)
logits = m(x)
logits 
 
>> tensor([[-0.2135, -0.0248,  3.985, -4.235, -0.1831]], grad_fn=<AddmmBackward0>)

scores = torch.softmax(logits)
scores 

>> tensor([[0.0096, 0.0117, 0.9765, 0.0002, 0.0020]], grad_fn=<SoftmaxBackward0>)
위에서 볼 수 있듯이, 로짓은 딥러닝 모델이 내는 원시 출력입니다. 엠 주어진 입력 이미지가 있을 때 엑.
앞서 언급했듯이, 로짓은 음의 무한대부터 양의 무한대까지 모든 실수 범위의 값을 가질 수 있습니다.
💡
이 로짓들은 이후 softmax와 같은 정규화 함수로 전달되며, 그 출력은 (0, 1) 범위에만 속하고 모든 값의 합이 1이 됩니다.

소프트맥스 출력의 단계별 계산

이제 소프트맥스 함수에 대해 자세히 이해하고 살펴보겠습니다.
softmax(Zi)=exp⁡(Zi)∑nexp⁡(Zj)\text{softmax}(Z_{i}) = \frac{\exp(Z_i)}{\sum_n \exp(Z_j)}

주어진 입력 벡터가 있을 때 ZZ, 소프트맥스 값의 ZiZ_i 와 같다 eZi/(eZ1+eZ2+...+eZn)e^{Z_i}/(e^{Z_1} + e^{Z_2} + ... + e^{Z_n}) 총합이 있다고 가정하면 NN 입력 벡터의 원소들 Z.Z.
그럼, 이전에 TIMM으로 만든 신경망의 원시 출력값(로그릿)에 소프트맥스를 적용해 봅시다.
원시 출력 로짓이 벡터에 저장되어 있다고 가정해 봅시다 엑스. 이 벡터의 첫 번째 원소에 대한 소프트맥스 값을 계산하고자 합니다.
X=[−0.2135,−0.0248,3.985,−4.235,−0.1831]X = [-0.2135, -0.0248, 3.985, -4.235, -0.1831]
수학적 공식에 따르면:
softmax(−0.2135)=e−0.2135e−0.2135+e−0.0248+e3.985+e−4.235+e−0.1831\text{softmax}(-0.2135) = \frac{e^{-0.2135}}{e^{-0.2135} + e^{-0.0248} + e^{ 3.985} + e^{-4.235} + e^{-0.1831}}
먼저 각 항의 지수를 개별적으로 계산합니다:
e−0.2135e^{-0.2135}≈0.8073
e−0.0248e^{-0.0248}≈0.9754
e0.3985e^{0.3985} ≈53.7032
e−0.4235e^{ −0.4235}≈0.0144
e−0.1831e^{−0.1831}≈0.8327
그다음 지수의 최종 합은 *= 56.3330 입니다.
그러므로, Softmax(−0.2135)=0.8073/56.3330=0.0096\text{Softmax}(-0.2135) = 0.8073/56.3330 = 0.0096
따라서 첫 번째 요소에 대한 softmax 활성화 함수의 출력은 -0.2135 는 0.0096
소프트맥스 함수의 몇 가지 성질:"
  1. 대부분의 분류 문제에서 마지막 정규화 층으로 쓰이는 이유는, 모델이 결국 “하나를 고르도록” 만들기 위해서입니다.
  2. 출력은 항상 … 사이에 있어야 합니다. 0 그리고 1.
  3. 소프트맥스 함수의 출력 확률의 합은 항상 다음과 같습니다 1.
  4. 이 함수는 미분 가능하므로 역전파와 같은 그래디언트 기반 최적화 방법에 사용할 수 있습니다.
  5. 로짓(실수 값 벡터)을 확률 분포로 변환하는 방법으로 볼 수 있습니다.

소프트맥스 활성화 함수는 단일 클래스를 선택하려고 합니다

첫 번째 요점을 살펴보겠습니다. 이는 소프트맥스 함수를 직관적으로 이해하는 데 있어 가장 중요한 내용 중 하나입니다. Jeremy Howard가 널리 공유했듯이, fast.ai 코스:


소프트맥스 함수는 하나를 고르고 싶어 합니다. 왜일까요? 어떤 값의 지수는 매우 빠르게 증가하기 때문입니다!
예를 들어, e4=54.5981e^4 = 54.5981 반면에 e8=2980.9579e^8=2980.9579그러므로 로짓이 있다면, 하나의 로짓이 다른 값들보다 조금만 더 크더라도, 그에 대한 소프트맥스 값은 다른 값들보다 훨씬 크게 됩니다.
어떤 로짓들이 주어졌다고 해봅시다 [0.02, -2.49, 1.25], 이 값들의 지수는 다음과 같습니다 [1.02, 0.08, 3.49]. 소프트맥스 값은 [0.22, 0.02,. 0.76]. 로짓의 소프트맥스가 어떻게 되는지 볼 수 있습니다 1.25 다른 모든 것보다 훨씬 더 큽니다.
그리고 이건 좋은 거죠. 왜냐하면 “이 이미지에 있는 반려동물의 품종은 무엇인가요?”처럼 모델에 질문할 때, 모델이 한 가지 품종을 딱 선택하길 원하기 때문입니다. 소프트맥스가 바로 그 역할을 합니다.

음의 로그 우도

이전에 시그모이드와 소프트맥스 활성화 함수들을 살펴봤으니, 이제는 로스 함수로 넘어가 보겠습니다. 구체적으로는 PyTorch의 로스를 다뤄보겠습니다. torch.nll_loss 음의 로그 우도 손실 함수입니다.
이제 본격적으로 들어가기 전에, 모델이 실제로 무엇을 최적화하려 하는지 살펴보겠습니다. 우리는 모델이 로스를 최소화하도록 만들고 싶습니다. 그렇다면 다중 클래스 분류 문제에서는 이것이 어떻게 작동할까요?
다음과 같은 문제 정의를 다루고 있다고 가정해 봅시다:
”회색곰, 테디베어, 갈색곰 중 하나에 해당하는 다섯 장의 이미지가 주어졌고, 각 이미지를 올바른 클래스에 분류하는 것이 당신의 과제입니다.
이걸 PyTorch 코드에서 어떻게 보이는지 살펴보겠습니다.
import torch, timm 
import torch.nn.functional as F

classes = ['Grizzly', 'Brown', 'Teddy']
targets = [1, 0, 2, 0, 2] # these are your labels
[classes[idx] for idx in targets]
>> ['Brown', 'Grizzly', 'Teddy', 'Grizzly', 'Teddy']
이는 레이블에 따르면 첫 번째 이미지는 …라는 뜻입니다. 갈색곰그리고 두 번째 이미지는 …입니다 그리즐리, 그리고 계속해서 
m = timm.create_model('resnet18', num_classes=3, pretrained=True)
x = torch.randn(5, 3, 224, 224) # five images of three channels of shape 224x224
logits = m(x)
logits

>>
tensor([[ 0.1752,  0.0539, -0.0581],
        [ 0.0544,  0.0642,  0.0782],
        [ 0.3230,  0.0958,  0.1941],
        [ 0.1143, -0.0508,  0.0701],
        [ 0.1249,  0.0510,  0.1147]], grad_fn=<AddmmBackward0>)
위에서 보았듯이, 로짓(logits)은 딥러닝 모델의 마지막 층에서 직접 나오는 가공되지 않은 출력값으로, 범위는 [−R,R][-R, R].
outputs = torch.softmax(logits, dim=1)
outputs 

>> 
tensor([[0.3734, **0.3308**, 0.2957],
        [**0.3296**, 0.3329, 0.3375],
        [0.3737, 0.2978, **0.3285**],
        [**0.3566**, 0.3023, 0.3411],
        [0.3426, 0.3182, **0.3391**]], grad_fn=<SoftmaxBackward0>)

idxs = torch.arange(5)
-outputs[idxs, targets]
>> tensor([-0.3308, -0.3296, -0.3285, -0.3566, -0.3391], grad_fn=<NegBackward0>)
이제 손실 함수 관점에서는, 우리의 타깃을 기준으로 위에서 강조된 값들에 주목합니다 [1, 0, 2, 0, 2]이 값들의 음수를 취하면 negative log-likelihood(NLL)라고 부릅니다. 이상적으로는 이 값들이 가장 크고 1에 가깝기를 원합니다.
이 값들의 음수를 취하면, PyTorch에서는 이를 다음과 같이 부릅니다 F.nll_loss. 
F.nll_loss(outputs, targets, reduction='none')

>> tensor([-0.3308, -0.3296, -0.3285, -0.3566, -0.3391], grad_fn=<NllLossBackward0>)
위에서 보았듯이, 출력은 F.nll_loss 은(는) 앞서 강조된 값들의 음수입니다.
위에서는 로그를 취하지 않았다는 점에 유의하세요. -outputs[idxs, targets] 위에서 보인 것처럼 F.nll_loss와 동일합니다. PyTorch에서는 softmax 출력에 로그를 취한 뒤 F.nll_loss를 적용하는 것이 훨씬 빠르기 때문입니다.
💡

크로스 엔트로피 손실

로짓에 소프트맥스를 적용한 뒤 로그를 취한 값으로 이어집니다 F.nll_loss 는 Cross Entropy Loss라고 합니다.
복잡하게 들리나요? 단계별로 나누면 그렇지 않습니다. 아래의 네 가지 단계가 Cross-Entropy Loss의 완전한 정의입니다.
  1. 로짓 계산하기(모델 최종 층에서 나온 원시 출력)
  2. 로짓에 소프트맥스를 적용하세요.
  3. 2단계에서 얻은 출력에 로그를 취하세요.
  4. 계산하기 F.nll_loss 이는 앞서 보여준 것처럼 단순히 인덱싱을 수행하는 것으로, 3단계의 출력과 타깃 값을 함께 전달하면 됩니다.
이제 코드를 통해 확인해 봅시다.
import torch, timm 
import torch.nn.functional as F

############################## step=1 ##############################
classes = ['Grizzly', 'Brown', 'Teddy']
targets = [1, 0, 2, 0, 2] # these are your labels
m = timm.create_model('resnet18', num_classes=3, pretrained=True)
x = torch.randn(5, 3, 224, 224) # five images of three channels of shape 224x224
logits = m(x)
logits
>>
tensor([[ 0.1752,  0.0539, -0.0581],
        [ 0.0544,  0.0642,  0.0782],
        [ 0.3230,  0.0958,  0.1941],
        [ 0.1143, -0.0508,  0.0701],
        [ 0.1249,  0.0510,  0.1147]], grad_fn=<AddmmBackward0>)
이제 우리 모델에서 나온 원시 출력(로짓)을 확보했습니다.
############################## step=2 ##############################

torch.softmax(logits, dim=1)
>> 
tensor([[0.3734, 0.3308, 0.2957],
        [0.3296, 0.3329, 0.3375],
        [0.3737, 0.2978, 0.3285],
        [0.3566, 0.3023, 0.3411],
        [0.3426, 0.3182, 0.3391]], grad_fn=<SoftmaxBackward0>)
좋아요. 다음 단계에 따라 로그를 취해야 합니다. 
############################## step=3 ##############################
torch.log(torch.softmax(logits, dim=1))
>> 
tensor([[-0.9850, -1.1062, -1.2183],
        [-1.1099, -1.1001, -1.0861],
        [-0.9842, -1.2115, -1.1132],
        [-1.0312, -1.1963, -1.0755],
        [-1.0711, -1.1450, -1.0813]], grad_fn=<LogBackward0>)
마지막으로, PyTorch를 사용해 타깃과 3단계의 출력을 전달하여 negative log likelihood를 계산합니다. 
############################## step=4 ##############################
F.nll_loss(torch.log(torch.softmax(logits, dim=1)), torch.tensor(targets), reduction='none')

>> tensor([1.1062, 1.1099, 1.1132, 1.0312, 1.0813], grad_fn=<NllLossBackward0>)
이것은 Cross Entropy Loss와 동일합니다.! 이제 PyTorch를 사용해 Cross Entropy Loss의 출력과 비교해 봅시다. 
import torch.nn as nn
loss_fn = nn.CrossEntropyLoss(reduction='none')
loss_fn(logits, targets)

>> tensor([1.1062, 1.1099, 1.1132, 1.0312, 1.0813], grad_fn=<NllLossBackward0>)
보시다시피 출력이 동일합니다! 따라서 Cross Entropy Loss를 단계별로 성공적으로 계산했습니다! 앞서 언급했듯이, “로짓에 소프트맥스를 적용한 뒤 로그를 취한 값으로 이어집니다 F.nll_loss 는 Cross Entropy Loss라고 합니다.”
PyTorch에는 다음과 같은 함수가 제공된다는 점에 유의하세요. torch.log_softmax 대신으로 사용할 수 있는 torch.log(torch.softmax(...)).
💡

결론

이 블로그 글에서는 딥러닝 맥락에서 로짓이 무엇을 의미하는지 설명했습니다. 간단히 말해, 로짓은 딥러닝 네트워크의 마지막 층에서 나오는 가공되지 않은 원시 출력값입니다.
다음으로, Sigmoid와 Softmax 활성화 함수도 살펴보았습니다. Sigmoid 활성화 함수는 모든 원시 값을 다음 범위의 점수로 변환할 수 있습니다: (−1,1)(-1, 1). Softmax도 동일한 작업을 수행할 수 있지만, 출력값들의 합이 1이 되도록 보장합니다. 따라서 이진 분류 및 멀티라벨 분류 문제에는 sigmoid가 선호되고, 모델이 “하나의 클래스를 선택”하길 원하는 멀티클래스 분류 문제에는 softmax가 선호됩니다.
마지막으로, PyTorch의 negative log-likelihood 함수를 살펴보고 4가지 간단한 단계로 Cross-Entropy Loss를 계산해 보았습니다! 이를 통해 독자분들이 이 개념들을 명확하고 또렷하게 이해하시길 바랍니다. 🙂


이 글은 AI로 번역되었습니다. 오역이 의심되는 부분이 있으면 댓글로 알려 주세요. 원문 링크는 여기에서 확인하실 수 있습니다: 원문 보고서 보기

Created with ❤️ on Weights & Biases.

https://wandb.ai/wandb_fc/korean/reports/---VmlldzoxNDM2NDk1OA
Made with Weights & Biases. Sign up or log in to create reports like this one.