How the OpenAI Robotics Team Uses W&B Reports
On the Robotics team at OpenAI, we have heavily adopted W&B Reports into our workflow and over the last ~6 months have shifted to using them as our primary means of sharing results within the team.
The ability to mix real data from experiments with context and commentary on the results was the primary selling point for us; prior to Reports, we typically would create a Google Doc for tracking all of the “runs” in a given line of experimentation and would have to spend a fair amount of time properly linking these docs to the experimental data (either in Weights & Biases or Tensorboard).
Reports save us from this tedious bookkeeping while also allowing us to more easily share complete views on the data (since the viewer can select which runs to view, drill into specific runs, or even clone the report to add more plots).
Workflow with Reports
Whenever we begin a new line of experimentation (e.g. batch size ablations, architecture search), we tend to use the following workflow with Reports:
Step 1: Create a new report with text at the top explaining the context, hypotheses under test, and experimental plan; then share this with the team for review. Doing this helps to bring more rigor to the experimental process, and helps teammates to spot issues or suggest ideas earlier on.
Step 2: Launch one or more experiments aimed at testing the hypotheses.
Tip: log the git SHA used to kick off each experiment or use Weights & Biases’ code logging feature; we tend to include the Git SHA prefix in experiment names for easy access
Step 3: Once the experiments are confirmed to be running correctly (i.e. no visible bugs), we add each as its own Run Set, and then add a number of plots for all the metrics we care about. Doing this up front makes it easy to monitor in-flight experiments, particularly when you have many running concurrently.
Tip: descriptively name Run Sets and make all runs in each Run Set within a given section the same color
Step 4: Monitor the experiments. If enough data has been collected after the first set of experiments, add a conclusion to the top and share with the team. Otherwise, update the hypotheses and experimental plan and return to step 2.
The rest of this Report presents one example of this workflow applied to the line of research aimed at solving the block reorientation task from our Learning Dexterity release in an end-to-end manner (there is of course a bit more context included here compared to internal reports). If you are unfamiliar with this work, I suggest reading through the collapsed “Background” section below.
Background
In Learning Dexterity, we trained a human-like robot hand to manipulate physical objects with unprecedented dexterity. Specifically, the hand was able to reorient a wooden block into a desired position and orientation with a high rate of success. Last November, in Solving Rubik’s Cube, we leveraged an evolution of this basic approach to manipulate Rubik’s cube with the same robotic hand.
For both of these releases, we decomposed the learning problem into two parts:
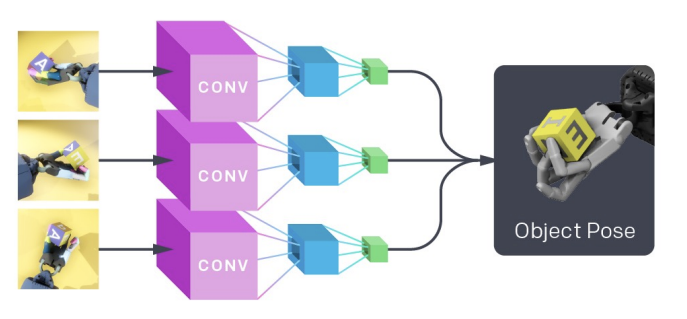
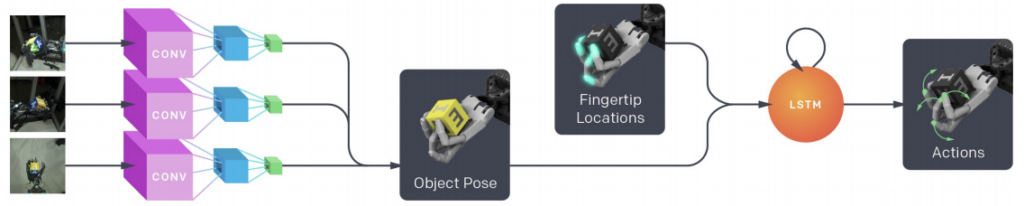
1. Learning a vision model, via Supervised Learning, which maps image observations from cameras mounted around the robot to give estimates of the block’s pose:
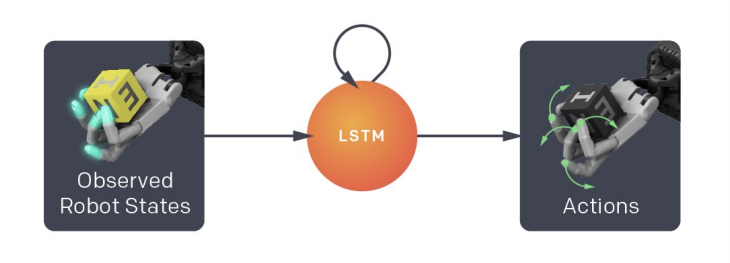
2. Learning a goal-conditioned policy, via Reinforcement Learning, which uses the estimates from the vision model (as well as a desired goal state) to produce commands used to control the robotic hand:
3. Both of these models are learned entirely in simulation. In order to allow these models to transfer to the real world, we employ Domain Randomization on the training distribution for each. For the policy, this involves training with a wide variety of simulator physics (e.g. different gravitational constants, coefficients of friction, etc.). For the vision model, we use OpenAI Remote Rendering Backend (ORRB) to render high-quality images of the scene with various aspects of the appearance randomized; here are some sample images:

When it comes time to experiment on the robot in the real world, we combine the vision model and policy:
Reinforcement Learning vs. Behavioral Cloning
Context
Once we shipped the Rubik’s cube results, we wanted to do an investigation into whether we could reduce the learning problem to a single step by learning a policy directly from images (aka “end-to-end“), resulting in a policy which looks like this:
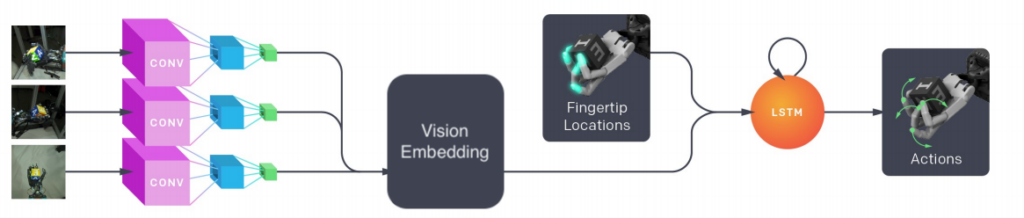
There are advantages to learning end-to-end (e.g. no need to design explicit state representations, conceptual simplicity), and knowing how well it would have worked for our recent releases could help inform future research directions. We decided to constrain this investigation to the setup from Learning Dexterity, i.e. block reorientation, for the sake of simplicity.
Hypotheses/Research Questions
Plan
-
Attempt to use Behavioral Cloning to train an end-to-end policy. Iterate on various aspects, such as using a pretrained vision model, batch size, vision model architecture, etc.
Conclusions
-
We found that we can use Behavioral Cloning to (relatively) efficiently train an end-to-end policy by using a pretrained state-based policy as the “teacher”. Part 1 below details our findings here, including ablations on model size, batch size, and the use of a pretrained vision “sub-model”. The most notable finding here is that using a pretrained vision sub-model speeds up training 4x.
-
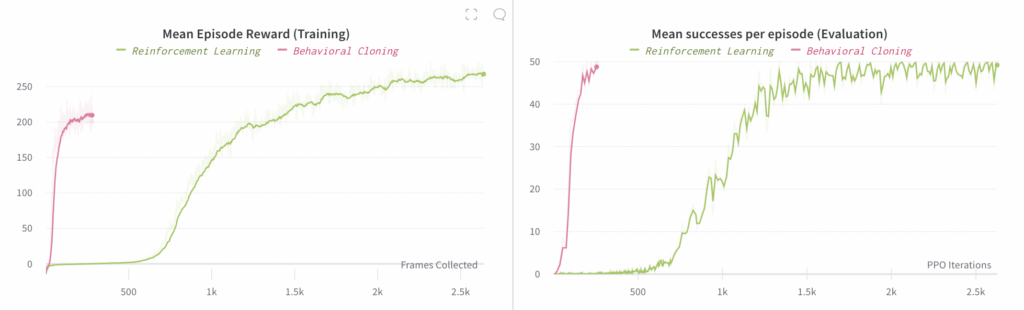
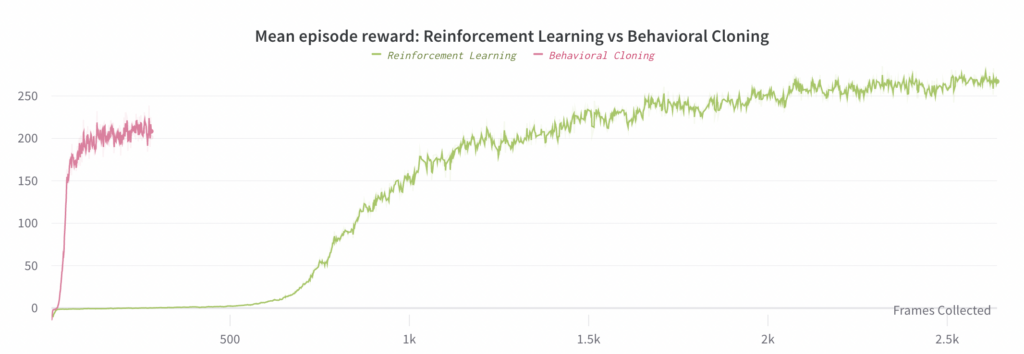
We can also use Reinforcement Learning to learn an end-to-end policy, but doing so requires ~30x more compute than Behavioral Cloning (when both use a pretrained vision sub-model). Part 2 details this experiment and compares it to the best Behavioral Cloning experiment (the main result is in the below plot)
Part 1: Behavioral Cloning
Within the Robotics team at OpenAI, we frequently use Behavioral Cloning to quickly train policies using an already-trained policy. We found this useful in a few scenarios, including jump-starting the training of a policy with a different model architecture or observation space; see section 6.4 of the Rubik’s cube paper for details. Thus, it was natural for us to begin this investigation by seeing if we could clone a state based policy into an end-to-end policy.
Fortunately, we found that Behavioral Cloning works very well for training end-to-end policies. Since Behavioral Cloning is effectively a form of Supervised Learning, we can use much smaller batch sizes and require far fewer optimization steps to train the end-to-end policies to convergence, relative to Reinforcement Learning. This is particularly beneficial when training end-to-end policies, since the maximum batch size per GPU is much smaller than state-based policies (due to the much larger observations and large size of vision model activations).
For these experiments, we additionally leveraged the original supervised state prediction learning task to pretrain the vision sub-model (i.e., we trained the vision model to convergence on that task, and then used the resulting parameters up through the penultimate layer to initialize the vision sub-model in the end-to-end policies).
In the following subsections, we present the results of a few interesting ablation experiments we ran with Behavioral Cloning; here are the conclusions:
-
Model architecture: we tried two different architectures for the vision sub-model, ResNet50 and the larger vision encoder from IMPALA, and found ResNet50 to perform better both in terms of compute required to converge as well as final performance.
-
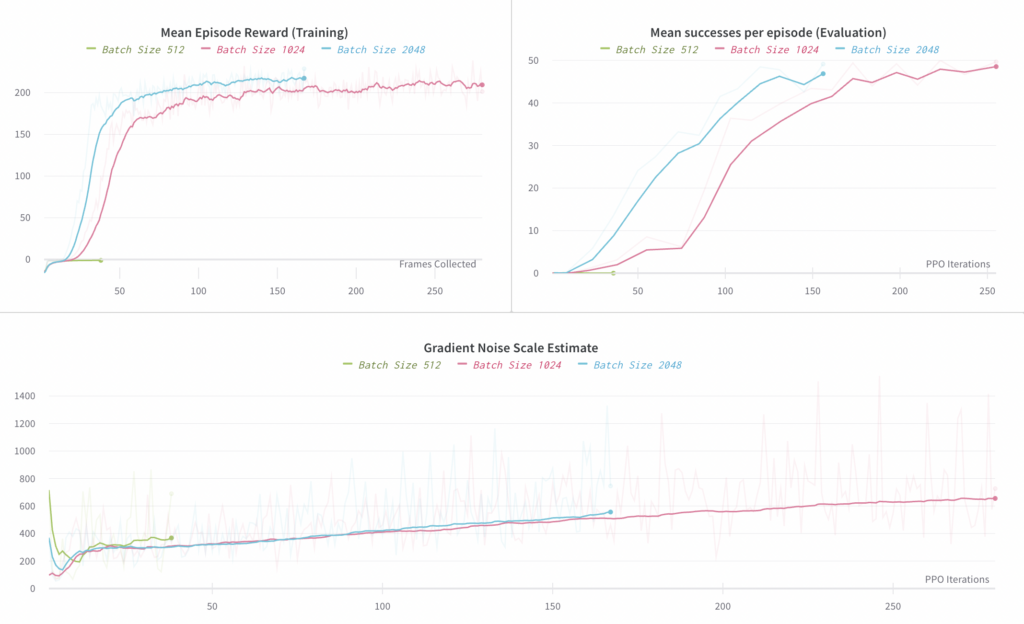
Batch Size: we tried total effective batch sizes of 512, 1024, and 2048 (achieved by scaling the number of GPU optimizers), and found 1024 to deliver the best compute efficiency while still achieving the maximum final performance.
Behavioral Cloning Ablation 1: Learning separate embedding mappings
As described in section 6.2 of the Rubik’s cube paper, we embed all inputs to the policy and value function networks into a 512-d space, sum them, and apply a nonlinearity prior to passing them on to the policy and value function networks:
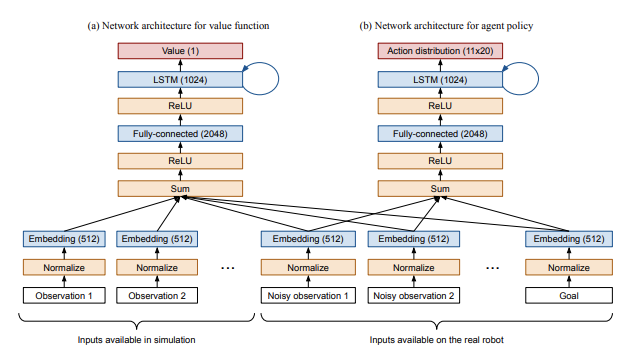
With our end-to-end policy, we started by using the same setup, just with different observations available to the policy network; specifically, we removed state observations and added an observation from the output of the vision sub-model. Note that the vision sub-model output is treated in the same manner as any other input, i.e. we apply a fully connected layer on it to embed it in the same 512-d space as all other inputs. We call these fully connected layers “embedding mappings”.
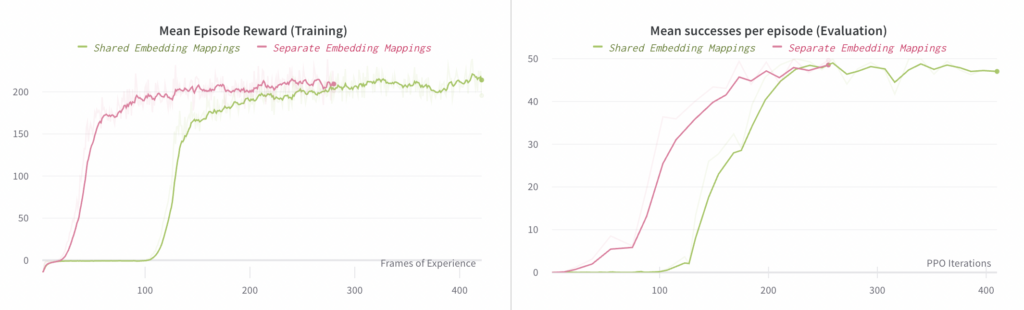
In the Rubik’s cube release, we shared these embedding mappings between the policy and value function networks. However, we found that when training end-to-end policies, learning separate embedding mappings is ~2-3x faster. We believe that this is due to interference between optimization of the value function and policy networks: since the value function still has access to full state information, it does not need the (relatively noisy) output from the vision sub-model, so it pushes the vision embedding towards zero. The policy network, of course, needs this vision embedding in order to understand the state of the environment; hence the conflict.
Below, we compare the progress of experiments with separate and shared embedding mappings. The plot on the left compares the mean reward observed in rollouts of the end-to-end policy (where these rollouts are used for training). The plot on the right compares the mean number of successes per episode, where a “success” involves reorienting the block to a desired goal; each episode is capped at a maximum of 50 successes.
Note that the left-hand plot’s x-axis is # Frames Collected (i.e. the amount of data consumed) whereas the right-hand plot’s x-axis is # PPO Iterations (i.e. how many steps of optimization).
Tip: spending a bit of time up-front to write good titles, add appropriate smoothing, and give consistent coloring goes a long way to saving teammates’ time reading the report.
Behavioral Cloning Ablation 2: Model Architecture
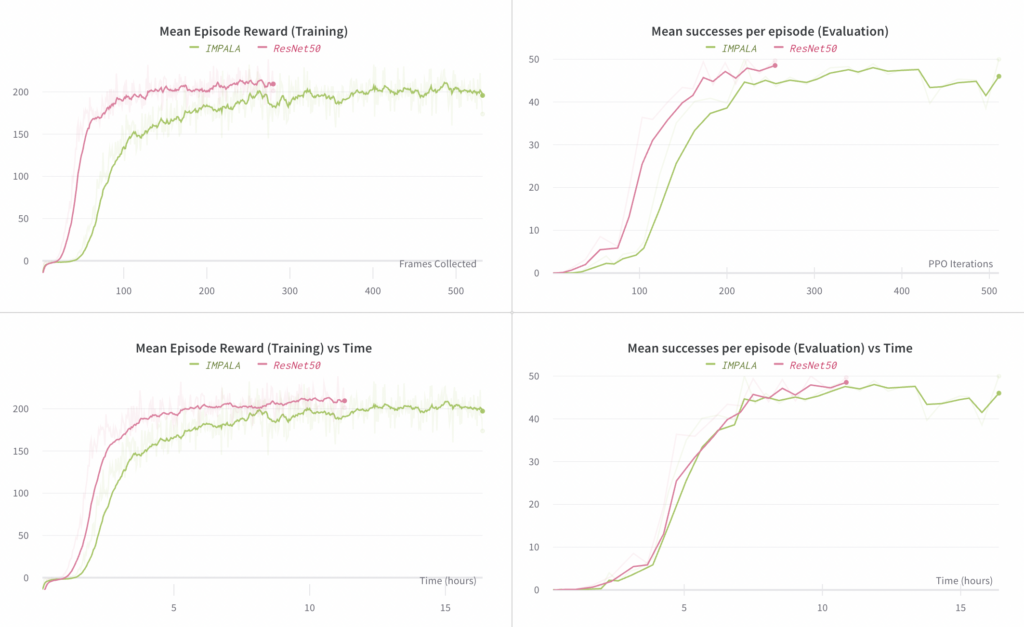
Here we ablate the choice of vision sub-model architecture. We compare using ResNet50 (as used in the Rubik’s cube release), with the much smaller IMAPALA vision encoder (the right image in figure 3 from the IMPALA paper). We found that the ResNet50 model results in slightly higher final performance (in terms of mean number of successes) relative to the IMPALA encoder, while requiring fewer steps to converge. The time per each step is slightly higher for the ResNet50 experiment, but it still converges more quickly in terms of elapsed time compared to the IMPALA experiment.
The plots on the left compare the mean reward observed in rollouts of the end-to-end policy (where these rollouts are used for training). The plots on the right compare the mean number of successes per episode, where a “success” involves reorienting the block to a desired goal; each episode is capped at a maximum of 50 successes.
Tip: duplicating sections removes some of the tedious work of setting up plots.
Behavioral Cloning Ablation 3: Batch Size
Here we ablate the total batch size used, comparing 512, 1024, and 2048. A batch size of 512 did not seem to work (we still saw negative mean reward after 38 steps, whereas we saw positive mean reward from the 1024 experiment after processing an equal number of samples). Batch sizes of 1024 and 2048 both worked, but the 2048 batch size only speeds up training by ~30%, so we consider 1024 to be optimal in terms of sample and compute efficiency. This is most easily observed in the first plot below of Mean Reward vs Frames Collected.
The plot on the left compares the mean reward observed in rollouts of the end-to-end policy (where these rollouts are used for training). The plot on the right compares the mean number of successes per episode, where a “success” involves reorienting the block to a desired goal; each episode is capped at a maximum of 50 successes.
Below, we plot an estimate of the Gradient Noise Scale, as described in “An Empirical Model of Large Batch Training”. We see that at convergence it is roughly 700, implying a critical batch size in that neighborhood. Note, however, that the behavior of the Gradient Noise Scale has not been as well studied for Behavioral Cloning, so we primarily used it here to get a rough understanding of what batch size we should target; for this it was useful, as it does correctly predict the optimal order of magnitude for the batch size.
Tip: some metrics are noisier than others, such as this one, so it is best to apply plot-specific smoothing.
Behavioral Cloning Ablation 4: Pretraining
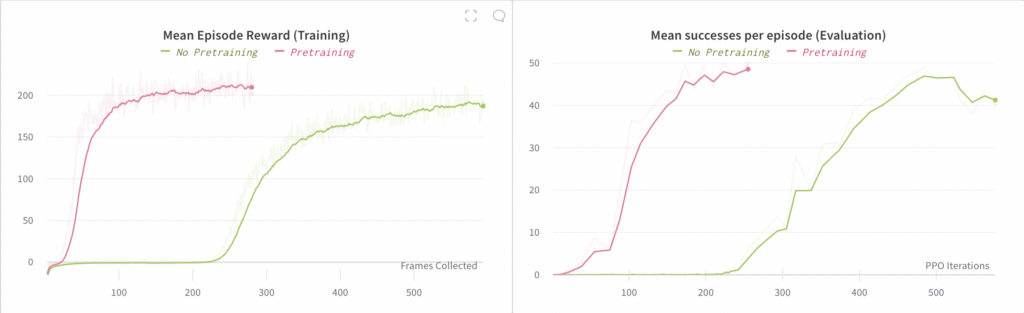
Here we ablate the use of a pretrained vision sub-model. We found that we are still able to train an end-to-end policy without using pretraining, but that it is 4x slower to converge.
The plot on the left compares the mean reward observed in rollouts of the end-to-end policy (where these rollouts are used for training). The plot on the right compares the mean number of successes per episode, where a “success” involves reorienting the block to a desired goal; each episode is capped at a maximum of 50 successes.
Part 2: Reinforcement Learning vs Behavioral Cloning
Once we completed the above ablations, we then took the best overall setup per the ablations and used it to train an end-to-end policy via Reinforcement Learning. Note that this also used a pretrained model as in the Behavioral Cloning experiments.
We found that training an end-to-end policy via RL does work; it is just quite a lot slower than Behavioral Cloning, which is to be expected. We only ran a single experiment here due to the much higher compute requirements: the RL experiment required 128 V100 GPUs for 4 days compared to the 48 V100 GPUs for 8 hours required by Behavioral Cloning. In total, this comes out to ~30x more compute for RL compared to Behavioral Cloning, and about 2.67x as much compute per step. The main value of this conclusion is that it tells us it is still possible to use RL to learn end-to-end policies, but that it will in general be very compute intensive unless we are able to find further optimizations.
Note that since the batch size used by the RL experiment is much larger, the shapes of the two below plots differ (since the left-hand plot uses an x-axis of Frames Collected).