Part 1: Deep Representations, a Way Towards Neural Style Transfer
This article provides a top-down approach to conceiving neural style transfer using Weights & Biases.
Created on September 1|Last edited on November 6
Comment
Artistic style transfer is an algorithm proposed by Gatys et al. In A Neural Algorithm of Artistic Style, the authors talk about the difficulties in segregating the content and style of an image. The content of an image refers to the discernible objects in an image. The style of an image, on the other hand, refers to the abstract configurations of the elements in the image that make it unique.
Style and content segregation is difficult because of the unavailability of representations that hold the semantic understanding of images. Now, due to the advancement of convolutional neural networks, such semantic representations are possible.

Aritra + Pablo = 🎨
This is part one of the two.
Table of Contents
Understanding Deep Image Representation by Inverting ThemNormalized VGG16Content RepresentationAmalgamationConclusion
The second part will talk about an image's style and how to extract it from an image.
Understanding Deep Image Representation by Inverting Them
This is the title of a research paper by Aravindh Mahendran et al. We think this paper is the root cause of artistic style transfer. In this paper, the authors dive deep into the interpretability of visual models. Their novelty lies in an algorithm that helps visualize deep image representation from a convolution neural network.
Idea: For any given task, a convolutional neural network builds representations of images in the intermediate layers. These representations stem from the different weights of filter kernels. The authors pose a pretty basic question and answer it themselves:
Given an encoding of an image, to which extent is it possible to reconstruct the image itself?
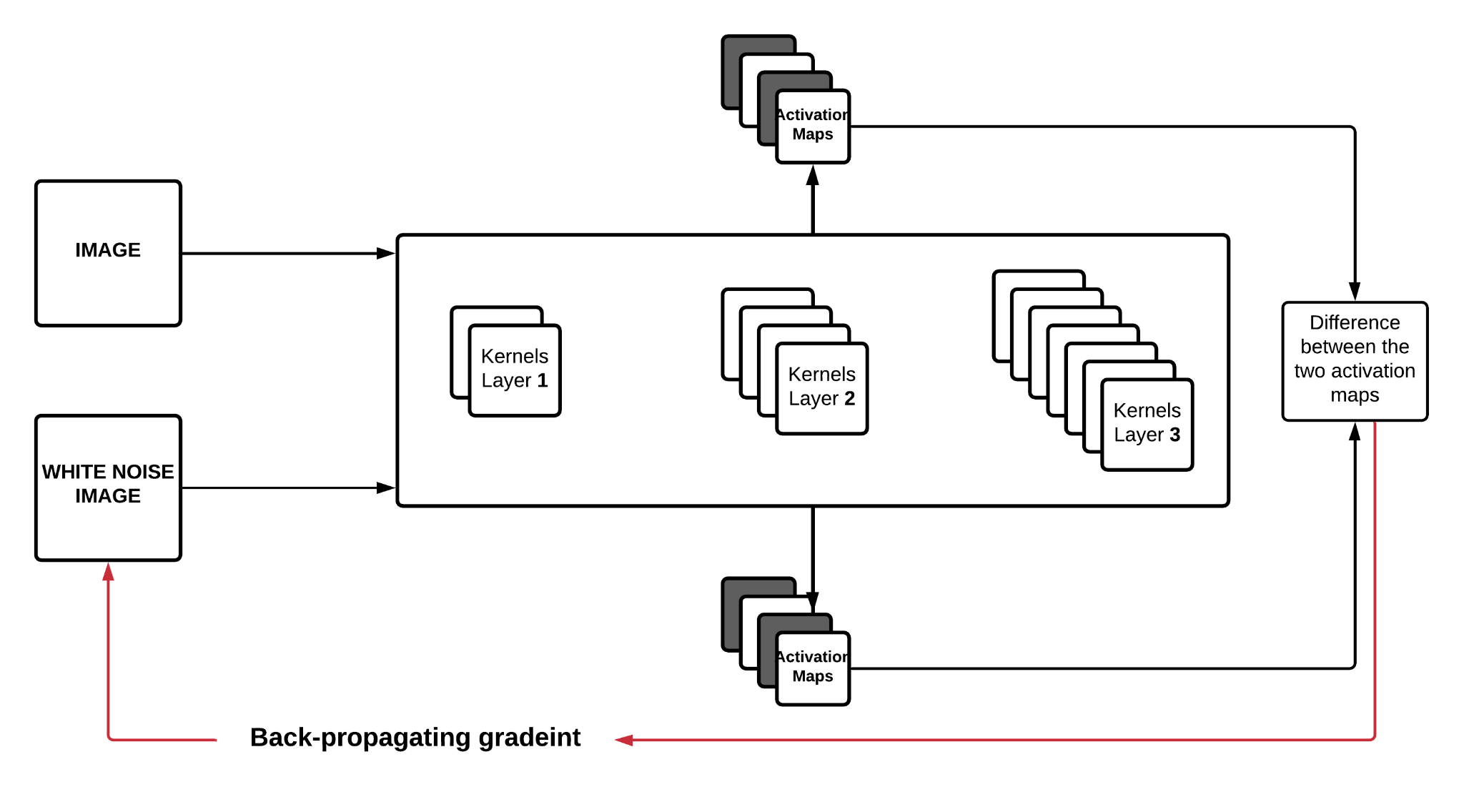
They take a pre-trained CNN, VGG16 trained on ImageNet, forward propagate an Image , and extract all the intermediate activation maps from the model. The activation maps of the image can be considered to be the encoding of that image. They also forward propagate a White Noise Image through the model and extract its activation maps . They argue that, if the loss between the activation maps of the original image and the white noise image is minimized by updating the white noise image pixels, the white noise image would resemble the original image.
The objective function becomes pretty simple:
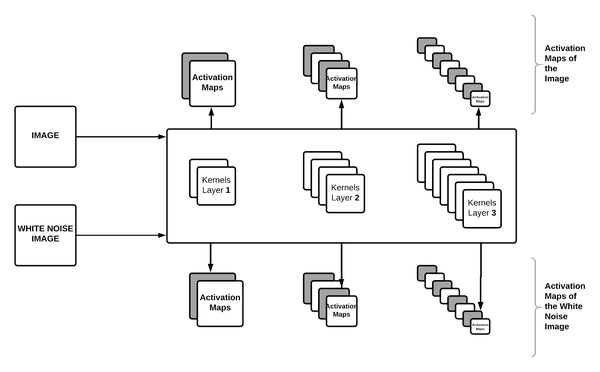
Convolutional layer with its activation maps and filter kernels
A note for the readers: In deep learning, we update the weights of neurons such that the modeling of input space helps the objective function. In this paper, the idea of updating the input itself makes it quite mesmerizing.
The authors visualize every convolutional layer, extract the Image and the White Noise Image's activation maps, and back-propagate the loss between the maps. The back-propagation does not update the weights of the filters but helps the white noise image update. The updated White Noise Image should give us the image that results in the activation maps of the original Image's chosen convolutional layer.
Normalized VGG16
We used the feature space provided by a normalized version of the 16 convolutional and 5 pooling layers of the 19-layer VGG network. We normalized the network by scaling the weights such that the mean activation of each convolutional filter over images and positions is equal to one. Such re-scaling can be done for the VGG network without changing its output because it contains only rectifying linear activation functions and no normalization or pooling over feature maps.
VGG16 architecture does not house any normalization layers. This has a downside; the activation maps are ReLU activated but do not have an upper bound to it. This means that the loss between the activation maps cannot be constrained to any range, which has an adverse effect on back-propagation and optimization. The authors devise a relatively simple scheme to normalize the architecture by scaling the weights themselves.
This StackOverflow thread sheds some light on how to normalize the weights. It is quite simple, a set of images are taken and forward propagated through the model. The activation maps are stored, and the mean is gathered. The weights and biases are then divided by this mean so that the activation provides normalized activation maps. A comment down at the bottom suggests that the paper's authors have normalized the model by using ImageNet’s validation images.
A smart catch comes from this StackOverflow thread where it is noticed that dividing by the activation mean does not sound right. The problem that we would face if weights and biases are merely normalized with the immediate activation means is that the input distribution to the next layers would disrupt. This calls for a method that takes care of the joint normalization of the weights and inputs. We have taken help from this repository. Here the weights are first multiplied to the mean of the previous convolutional layer’s mean and then are normalized with the mean of its activation maps.
All of the concepts of normalization boil down to these three lines of code.
# conv layer weights layout is: (dim1, dim2, in_channels, out_channels)W *= prev_conv_layer_means[np.newaxis, np.newaxis, : , np.newaxis]b /= meansW /= means[np.newaxis, np.newaxis, np.newaxis, :]
Content Representation

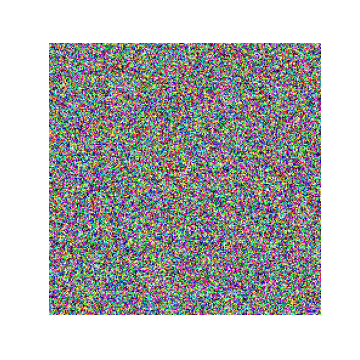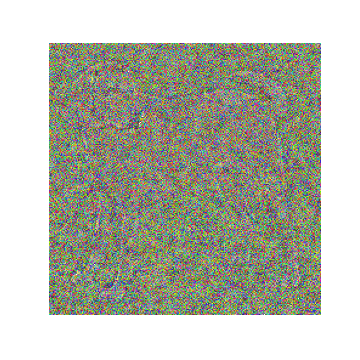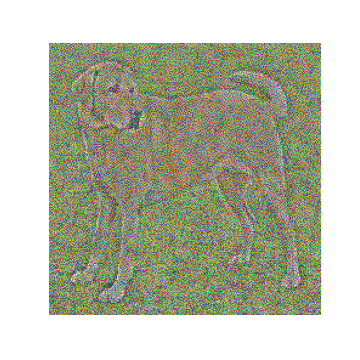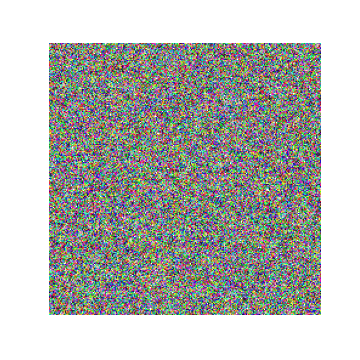
The algorithm of content representation of an image comes directly from the paper Understanding deep image representation by inverting them. We have already laid the foundations of the process in the section above. Here we will understand and visualize the steps.
We will take an Image from which content needs to be extracted. We take another image that is a White Noise Image. The objective of our algorithm is to extract the content from and imprint it upon . The best part about this idea is that the authors treat the problem as an optimization problem.
The optimization probelm: A layer with distinct filters has feature maps each of size , where is the height times the width of the feature map. So the responses in a layer can be stored in a matrix
where is the activation of the filter at position in layer . Let us consider a layer and forward propagate the two images and , the Image and the White Noise Image respectively. The activation maps at the layer are and . We can define the squared error loss between the two as
Here lie the optimization criteria. With an optimizer in place, this loss is considered to be minimized. As mentioned in a previous section, the loss is optimized by updating the White Noise Image .
We calculate the loss function's derivative with respect to the activation map of the White Noise Image $ A $.
With this in hand, we can easily back-propagate this derivation and then finally update the White Noise Image.
This process can be applied to every layer of the network at hand. In our experiments, we take the pre-trained VGG16 normalized model. We run our experiments on the conv1 layers of each block of the model. Below we see the transformation of the White Noise Images to the content Image .
Run set
5
Amalgamation
This section is very dear to us. This is not taken from any of the papers mentioned above. It is a set of elementary experiments that came naturally to us.
What if we used another image instead of the white noise image?
With this statement in mind, we went ahead and chose the style image and tried to imprint the content image on it.

The same mathematics applies here as well. The mean squared error between the two images is optimized, and the content of the content image is imprinted on the style image.
How so ever luring it might seem, but this is not Artistic Image Style Transfer. We have not segregated the style of the Style Image. Instead, we have just imprinted the content of the Content Image. Amalgamation is the term we chose in order to make the reader understand due process. This experiment results in the superimposition of the content of one image on the other image.
Run set
5
Conclusion
The first part deals with the content representations and the way we can visualize the embeddings of a convolutional neural network. We have kept this report as intuitive as possible for the readers to be creative about the process. We would like for you to figure a way out to harness the style information from an image.
In the next part of the report, we will be writing about the style representations. The way where we can understand the problem of texture transfer is in the realm of an optimization problem too. We would be more than happy to get your feedback on this report.
Reach the authors
| Name | Github | |
|---|---|---|
| Aritra Roy Gosthipaty | @ariG23498 | @ariG23498 |
| Devjyoti Chakraborty | @cr0wley-zz | @Cr0wley_zz |
Add a comment
Tags: Intermediate, Computer Vision, GenAI, Experiment, Research, CNN, Github, Panels, Plots, Slider, ImageNet
Iterate on AI agents and models faster. Try Weights & Biases today.
