On this page
MLOps 소개: 초매개변수 조정
Introduction
While the ingredients of a recipe play an important role, the instructions are just as important. Whether you bake a batch of cookies at 160°C for 20 minutes or at 180°C for 12 minutes can make a huge difference with the same ingredients.
So what does this have to do with machine learning (ML)? Well, in ML, the data, the preprocessing, and the model selection play an important role. But the model’s hyperparameters can significantly impact your ML model’s performance as well.
However, choosing the right hyperparameters for an ML model can be time-consuming. This article aims to give you an overview of what hyperparameters are, why it is important to tune them, how to tune them, and three different algorithms to automate hyperparameter optimization.
This is the second article in a small series of articles related to MLOps. Be sure to read the first article about Experiment Tracking in Machine Learning.
Let’s get started.
What are Hyperparameters in Machine Learning?
Hyperparameters are parameters that control the learning process. In contrast to other parameters, e.g., model weights, hyperparameters are not learned during the training process. Instead, you set them before training an ML model.
An example of a hyperparameter is the learning rate for training a neural network. Learning rate determines the step size at which the optimizer updates the model weights during training. A larger learning rate converges faster, but it can also cause the model to overshoot the optimal solution. A lower learning rate may take longer to converge, but it can help the model to find a better solution.
What is Hyperparameter Optimization in Machine Learning?
Hyperparameter optimization or hyperparameter tuning is the process of finding the best hyperparameters for an ML model. This is done by evaluating different sets of hyperparameter values from a specified search space to identify the best combination.
In the example of the learning rate, hyperparameter optimization aims to find a value that reaches the best solution in a given time frame (essentially finding the best trade-off between advantages and disadvantages of smaller and higher learning rate values).
Optimizing hyperparameters is essential because it can significantly impact a model’s performance. Different hyperparameter values result in different model performances.
How Do You Optimize Hyperparameters?
You can optimize hyperparameters manually or automatically. You can manually search for the best set of hyperparameters based on intuition and experience and through trial and error. Or you can use algorithms to automate this task for you. And automation is far more popular.
Before you begin with the hyperparameter tuning process, you need to define the following:
-
A set of hyperparameters you want to optimize (e.g., learning rate)
-
A search space for each hyperparameter either as specific values (e.g., 1e-3, 1e-4, and 1e-5) or as a value range (e.g., between 1e-5 and 1e-3 )
-
A performance metric to optimize (e.g., validation accuracy)
-
The number of trial runs (depending on the type of hyperparameter optimization, this can be implicit instead of explicit)
Before starting with automated hyperparameter optimization, you need to specify all of the above. But you can adjust the hyperparameter search space and the number of trial runs during manual hyperparameter tuning.
The generic steps for hyperparameter tuning are:
-
Select a set of hyperparameter values to evaluate
-
Run an ML experiment for the selected set of hyperparameters and their values, and evaluate and log its performance metric.
-
Repeat for the specified number of trial runs or until you are happy with the model’s performance
Depending on whether you manually conduct these steps or automate them, we talk about manual or automated hyperparameter optimization.
After this process, you will end up with a list of experiments, including their hyperparameters and performance metrics. An automated hyperparameter optimization algorithm returns the experiment with the best performance metric and the respective hyperparameter values.
During or after this process, you can compare the experiments’ performance metrics and choose the set of hyperparameter values that resulted in the best performance metric.
Methods for Automated Hyperparameter Optimization
The three main algorithms used in automated hyperparameter optimization are
-
Grid Search
The main difference between the three algorithms is how they select the set of hyperparameter values to test next. But they are also different in how you define the search space (fixed values vs. value ranges) and how you specify the number of runs (implicit vs. explicit).
This section will explore these differences and their advantages and disadvantages.
I will use W&B Sweeps to optimize the hyperparameters epochs and learning_rate in the following. For more details, you can check out my related Kaggle Notebook and W&B project.
Grid Search
Grid search is a hyperparameter tuning technique that evaluates all possible hyperparameter combinations in a specified grid (Cartesian product). It is a brute-force approach recommended only for ML models with few hyperparameters.
Inputs
-
A set of hyperparameters you want to optimize
-
A discretized search space for each hyperparameter either as specific values
-
A performance metric to optimize
-
(Implicit number of runs: Because the search space is a fixed set of values, you don’t have to specify the number of experiments to run)
(The differences between random search and Bayesian optimization are highlighted in bold above.)
A popular way to implement grid search in Python is to use GridSearchCV from the scikit learn library. Alternatively, as shown below, you can set up a grid search for hyperparameter tuning with W&B:
Steps
Step 1: The grid search algorithm selects a set of hyperparameter values to evaluate by creating a grid (cartesian product) of all possible hyperparameter combinations of the specified hyperparameter values. Then it simply iterates over the grid. This approach is an exhaustive search or brute force approach.
Below, you can see the resulting grid for our example.
Step 2: Run an ML experiment for the selected set of hyperparameters and their values, and evaluate and log its performance metric.
Step 3: Repeat for the specified number of trial runs or until you are happy with the model’s performance
Output
As with all automated hyperparameter optimization algorithms, Grid Search returns the experiment with the best performance metric and the respective hyperparameter values.
Below you can see at which time the hyperparameter optimization algorithm chose which parameters and the resulting performance. You can make the following observations:
-
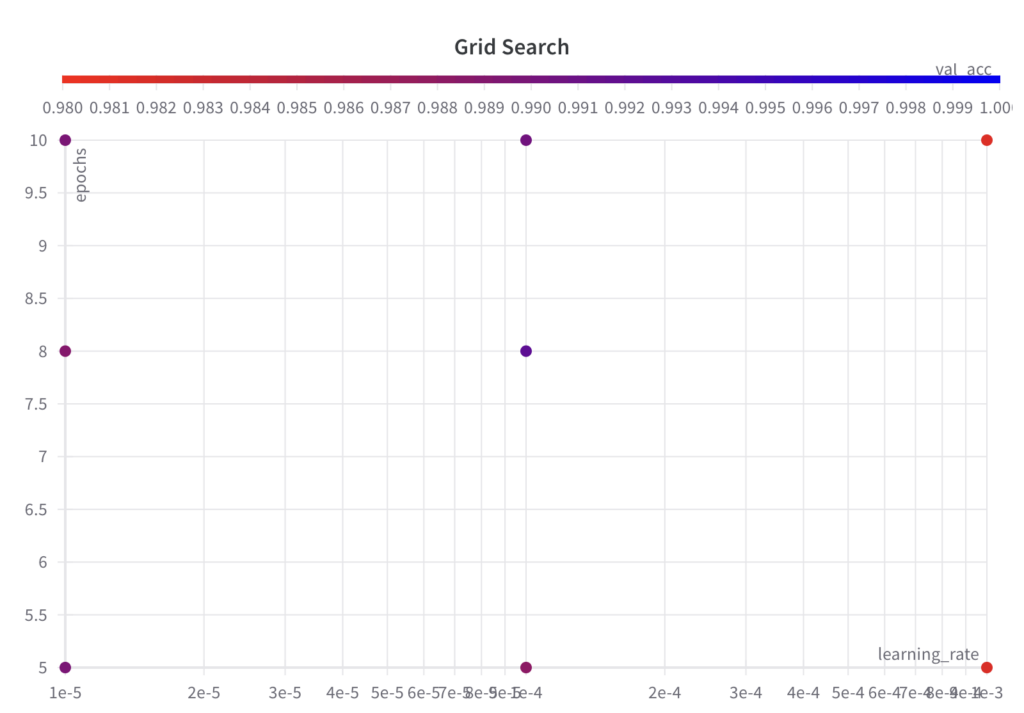
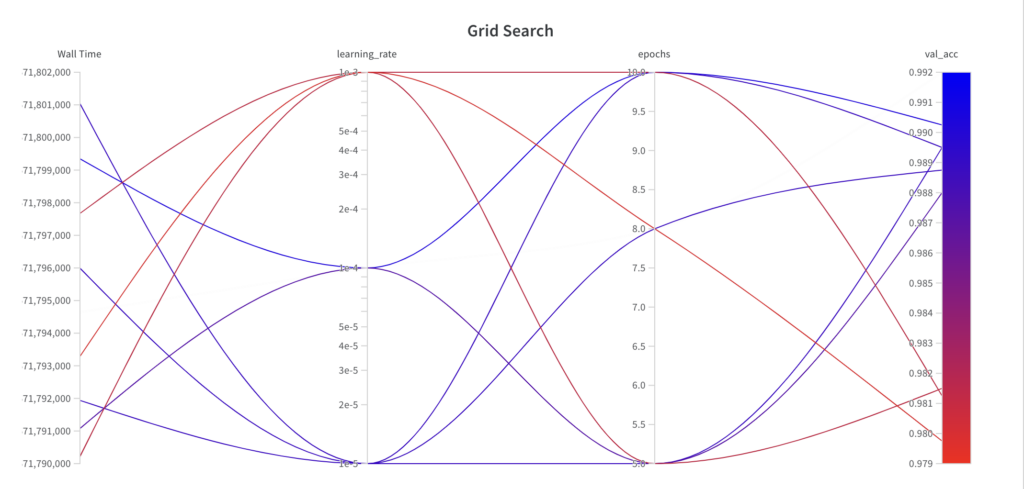
The grid search algorithm iterates over the grid of hyperparameter sets as specified.
-
Since grid search is an uninformed search algorithm, the resulting performance doesn’t show a trend over the runs.
-
The best val_acc score is 0.9902
Advantages
-
Simple to implement
-
Can be parallelized: because the hyperparameter sets can be evaluated independently
Disadvantages
-
Not suitable for models with many hyperparameters: this is largely because the computational cost grows exponentially with the number of hyperparameters
-
Uninformed search because knowledge from previous experiments is not leveraged. You may want to run the grid search algorithm several times with a fine-tuned search space to achieve good results.
Unless you have three or fewer hyperparameters to tune, it is generally recommended to avoid grid search.
Random Search
Random search is a hyperparameter tuning technique that randomly samples values from a specified search space. It is more effective than grid search for ML models with many hyperparameters where only a few affect the model’s performance [1].
Inputs
-
A set of hyperparameters you want to optimize
-
A continuous search space for each hyperparameter as a value range
-
A performance metric to optimize
-
Explicit number of runs: Because the search space is continuous, you must manually stop the search or define a maximum number of runs.
The differences to grid search are highlighted in bold above.
A popular way to implement random search in Python is to use RandomizedSearchCV from the scikit learn library. Alternatively, as shown below, you can set up a random search for hyperparameter tuning with W&B.
Steps
Step 1: The random search algorithm selects a set of hyperparameters to evaluate by randomly sampling hyperparameter values from the specified search space for each iteration for the number of specified iterations.
Below, you can see that the sampled sets of hyperparameter values do not follow a grid like in the grid search algorithm:
Step 2: Run an ML experiment for the selected set of hyperparameters and their values, and evaluate and log its performance metric.
Step 3: Repeat for the specified number of trial runs.
Output
As with all automated hyperparameter optimization algorithms, Random Search returns the experiment with the best performance metric and the respective hyperparameter values.
Below you can see at which time the hyperparameter optimization algorithm chose which parameters and the resulting performance. You can make the following observations:
-
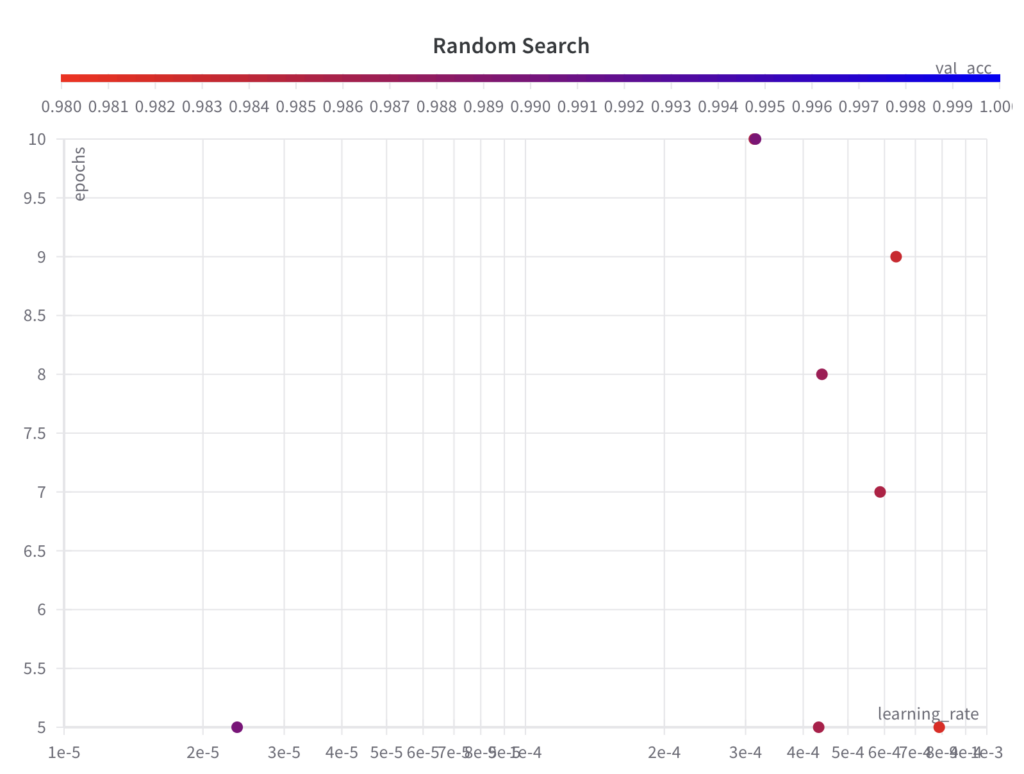
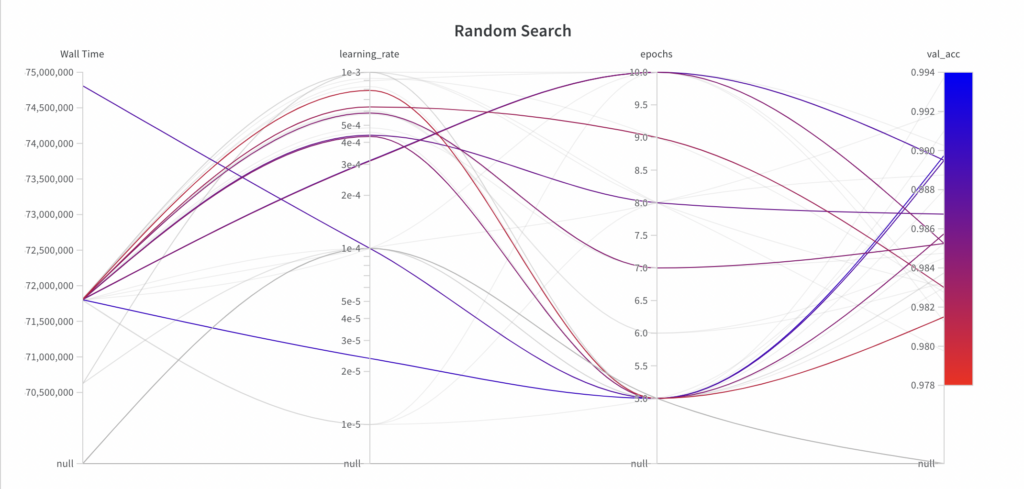
While random search samples values from the full search space for the hyperparameter epochs, it doesn’t explore the full search space for the hyperparameter learning_rate within the first few experiments.
-
Since random search is an uninformed search algorithm, the resulting performance doesn’t show a trend over the runs.
-
The best val_acc score is 0.9868, which is worse than the best val_acc score achieved with grid search (0.9902). The main reason for this is assumed to be the fact that the learning_rate has a large impact on the model’s performance, which the algorithm failed to sample properly in this example.
Advantages
-
Simple to implement
-
Can be parallelized: because the hyperparameter sets can be evaluated independently
-
Suitable for models with many hyperparameters: Random search is guaranteed to be more effective than grid search for models with many hyperparameters and only a small number of hyperparameters that affect the model’s performance [1]
Disadvantages
-
Uninformed search because knowledge from previous experiments is not leveraged. You may want to run the random search algorithm several times with a fine-tuned search space to achieve good results.
Bayesian Optimization
Bayesian optimization is a hyperparameter tuning technique that uses a surrogate function to determine the next set of hyperparameters to evaluate. In contrast to grid search and random search, Bayesian optimization is an informed search method.
Inputs
-
A set of hyperparameters you want to optimize
-
A continuous search space for each hyperparameter as a value range
-
A performance metric to optimize
-
Explicit number of runs: Because the search space is continuous, you must manually stop the search or define a maximum number of runs.
The differences in grid search are highlighted in bold above.
A popular way to implement Bayesian optimization in Python is to use BayesianOptimization from the bayes_opt library. Alternatively, as shown below, you can set up Bayesian optimization for hyperparameter tuning with W&B.
Steps
- Step 1: Build a probabilistic model of the objective function. This probabilistic model is called a surrogate function. The surrogate function comes from a Gaussian process [2] and estimates your ML model’s performance for different sets of hyperparameters.
- Step 2: The next set of hyperparameters is chosen based on what the surrogate function expects to achieve the best performance for the specified search space.
Below, you can see that the sampled sets of hyperparameter values do not follow a grid like in the grid search algorithm.
- Step 3: Run an ML experiment for the selected set of hyperparameters and their values, and evaluate and log its performance metric.
- Step 4: After the experiment, the surrogate function is updated with the last experiment’s results.
- Step 5: Repeat steps 2 – 4 for the specified number of trial runs.
Output
As with all automated hyperparameter optimization algorithms, Bayesian Optimization returns the experiment with the best performance metric and the respective hyperparameter values.
Below you can see at which time, the hyperparameter optimization algorithm chose which parameters and the resulting performance. You can make the following observations:
-
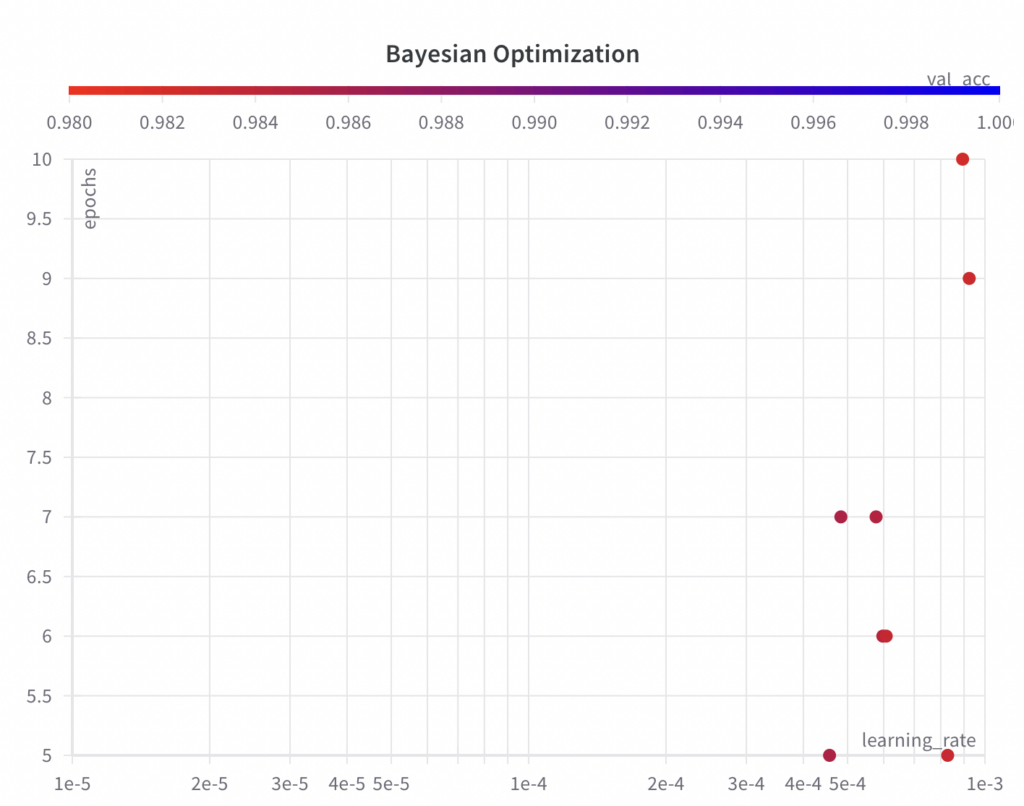
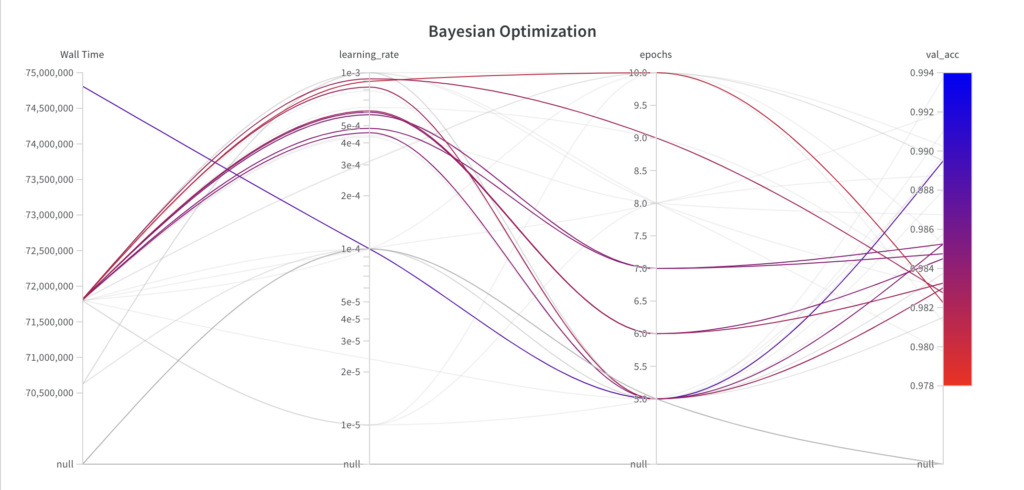
While the Bayesian optimization algorithm samples values from the full search space for the hyperparameter epochs, it doesn’t explore the full search space for the hyperparameter learning_rate within the first few experiments.
-
Since the Bayesian optimization algorithm is an informed search algorithm, the resulting performance shows improvements over the runs.
-
The best val_acc score is 0.9852, which is worse than the best val_acc score achieved with grid search (0.9902) and random search (0.9868). The main reason for this is assumed to be the fact that the learning_rate has a large impact on the model’s performance, which the algorithm failed to sample properly in this example. However, you can see that the algorithm has already begun to decrease the learning_rate to achieve better results. If given more runs, the Bayesian optimization algorithm could potentially lead to hyperparameters which result in a better performance.
Advantages
-
Suitable for models with many hyperparameters
-
Informed search: Takes advantage of knowledge from previous experiments and thus can converge faster to good hyperparameter values
Disadvantages
-
Difficult to implement
-
Can’t be parallelized because the next set of hyperparameters to be evaluated depends on the previous experiment’s results
Conclusion
Hyperparameter optimization is essential when developing an ML model because it can improve its performance. While you can tune hyperparameters manually, it is helpful to automate this task.
This article has discussed three popular methods of automated hyperparameter optimization: Grid search, random search, and Bayesian optimization.
Generally, the three automated hyperparameter tuning algorithms follow the same approach. They take a set of hyperparameters and their search spaces, a performance metric to optimize, and the number of trial runs as input. Then, a set of hyperparameter values is selected and evaluated in an ML experiment. All experiments’ results are logged to return the set of hyperparameter values with the best performance.
The main difference between the three algorithms is how they select the set of hyperparameter values to test next. Grid search evaluates all possible hyperparameter combinations in a specified grid (Cartesian product). Random search randomly samples values from a specified search space. Bayesian optimization uses a surrogate function to determine which set of hyperparameters to test next. In contrast to grid search and random search, Bayesian optimization is an informed search method.
The three methods are also different in how you define the search space and specify the number of runs. While Grid search takes fixed values to test, random search and Bayesian optimization take a continuous search space as input. Thus, you need to explicitly define the number of trials runs for random search and Bayesian optimization.
Finally, the three approaches can be compared regarding their advantages and disadvantages:
-
Bayesian optimization is more difficult to implement than grid search and random search.
-
Because Grid search is a brute-force approach, it is unsuitable for models with many hyperparameters like random search or Bayesian optimization.
-
In contrast to grid search and random search, Bayesian optimization is an informed search method and doesn’t have to be repeated with a fine-tuned search space to achieve good results.
-
But because Bayesian optimization is an informed search, it cannot be parallelized like the other two.
References
[1] Bergstra, J., & Bengio, Y. (2012). Random search for hyper-parameter optimization. Journal of machine learning research, 13(2).
[2] Weights & Biases Inc., (2022). Documentation: Define sweep configuration. (accessed 29. December 2022)